Abwickelbare Flächen in MultiSurf
Rumpf, Deck, Aufbau
von Reinhard Siegel
Inhalt
Einleitung
1 Was ist eine abwickelbare Fläche?
- 1.1 Grundformen – Zylinder, Kegel, Tangentenfläche
- 1.2 Die allgemeine abwickelbare Fläche – Kombination aus Zylinder, Kegel und Tangentenfläche
- 1.3 Regelfläche
2 Die Vorteile abwickelbarer Flächen
3 Abwickelbare Flächen mit MultiSurf
- 3.1 Developable Surface
- Bestimmung der Erzeugenden
- Breaklines
- Die Anordnung der Erzeugenden und ihr Einfluß auf den Strak
- 3.2 Straken von Developable Surfaces
- Allgemeine Hinweise
- Strahlenförmiger Verlauf der Erzeugenden
- Hinterkante mit Bucht
- Teilweise gerader Verlauf einer Stützkurve
- Stützkurve mit Wendepunkt
4 Rumpfentwurf mit abwickelbaren Flächen
- 4.1 Moderner Knickspanter
- 4.2 Klassischer Knickspanter
- 4.3 Motorboot
5 Besondere Rumpfformen
- 5.1 "Radius Chine"-Rumpf
- 5.2 Rumpf mit nichtabwickelbarer Teilfläche
- 5.3 Rumpf als Kegelfläche
6 Deck mit abwickelbarer Fläche
7 Aufbau mit abwickelbaren Flächen
8 Flächenabwicklung
- Expanded Surface
- Spiegelabwicklung
Einleitung
Muß bei der Konstruktion eines Bootes auf die Fertigungsmöglichkeiten des Erbauers und/oder auf wirtschaftliche Gründe (Kostenersparnis) Rücksicht genommen werden, wird für die Form des Rumpfes der Knickspant gewählt. Knickspanter sind nach landläufiger Meinung keine Freude für das Auge und haben gegenüber Rundspantformen einem höheren Widerstand. Da aber die Schönheit eines Bootes in der Hauptsache durch seine Proportionen bestimmt wird, sollten sich Knickspanter durchaus auch so entwerfen lassen, dass die Ästethik nicht zu kurz kommt. Und was das Leistungsvermögen angeht, so lassen sich besonders bei Verwendung mehrerer Knicke (Multiknickspant) Formen finden, die der rundspantigen Konkurrenz kaum nachstehen. Tatsächlich kann bei hohen Geschwindigkeiten (Motorboote) die Knickspantform hinsichtlich Widerstand und Seeverhalten dem Rundspant überlegen sein.
Nicht jeder Bootsrumpf in Knickspantform ist automatisch auch abwickelbar. Es ist ein weit verbreiteter Irrtum, zu glauben, ein Rumpf mit geradem Verlauf der Spanten zwischen Seite Deck, den Knickkurven und der Bodenkontur bestehe allein schon dadurch aus abwickelbaren Flächen. Vielmehr muß der Verlauf von Seite Deck, der Knickkurven und der Bodenkontur als Raumkurven ganz bestimmte Bedingungen erfüllen, damit sich zwischen ihnen strakende abwickelbare Flächen aufspannen lassen.
Was letztlich den Ausschlag geben mag, ein Boot als Knickspant zu bauen, es gibt keinen vernünftigen Grund, dabei nicht die Vorteile einer Flächenart zu nutzen, die überall in der Technik mit Erfolg verwendet wird.
Abwickelbare Flächen lassen sich für Außenhaut, Deck und Aufbauten einsetzen. Sie ermöglichen es auch dem Nichtfachmann, Material, Kosten und Zeit einzusparen und ein gutes Produkt zu erschaffen.
Verwendete Abkürzungen:
Cp: Kontrollpunkt, Stützpunkt (control point, support point)
Mc: Masterkurve, Stützkurve (master curve, support curve)
cp1, cp2, ...: bezeichnet den 1., 2. ... Punkt in der Liste der Kontrollpunkte einer Kurve. Es ist kein Objektname.
mc1, mc2, ...: bezeichnet die 1., 2. ... Kurve in der Liste der Stützkurven einer Fläche. Es ist kein Objektname.
Im Folgenden werden die MultiSurf-Namen für Punkt-, Kurven- und Flächenarten verwendet. Das ergibt zwar „denglische“ Sätze, soll aber dem Verständnis und der Nachvollziehbarkeit dienen.
1 Was ist eine abwickelbare Fläche?
Die Definition der abwickelbaren Fläche lautet in Worten:
"Eine gekrümmte Fläche heißt abwickelbar, wenn sie sich nur durch Verbiegung, also ohne Längenänderung der Flächenfasern, in eine Ebene ausbreiten läßt."
Eine solche Ausbreitung, Abwicklung oder Verebnung ist durchaus nicht für jede Fläche möglich. Ein Teil einer Kugeloberfläche kann nur mit Gewalt verebnet werden, wobei an den Rändern Dehnungen und Risse, in der Mitte Stauchungen und Falten entstehen. Bei Verebnung einer abwickelbaren Fläche treten dagegen ausschließlich Verbiegungen auf. Zwar wird im Schiffbau der Begriff Abwicklung im Zusammenhang mit der Bestimmung von Biegeschablonen und Lehren für die Außenhautplatten von rundspantigen Rumpfformen verwendet, was aber nichts zu tun hat mit abwickelbaren Flächen.
1.1 Grundformen - Zylinder, Kegel, Tangentenfläche
Ein einfaches Beispiel für einen Körper mit abwickelbarer Oberfläche ist eine Konservendose, geometrisch gesehen ein gerader Kreiszylinder (a). Schneidet man die Dose entlang des Bodens und Deckels sowie entlang des Mantels auf, läßt sie sich leicht verebnen. Man kann sie auch auf eine ebene Unterlage legen und einmal vollständig darauf abwälzen. Die Spur auf der Unterlage ist die Abwicklung des Dosenmantels: eine Rechteckfläche von gleicher Höhe wie die Dose und mit dem Dosenumfang als Seitenlänge). Ein weiteres Beispiel ist der gerade Kreiskegel (b). Wälzt man ihn auf einer ebenen Unterlage ab, erhält man die Abwicklung seines Mantels als Kreissegment.
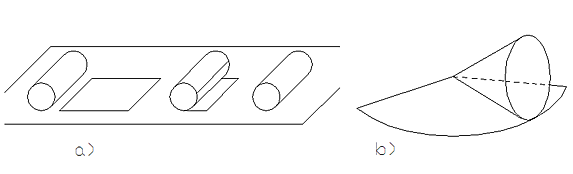
Einfache abwickelbare Flächen: gerader Zylinder und gerader Kreiskegel
Etwas kompliziertere Beispiele für abwickelbare Flächen sind die allgemeinen Zylinder- und Kegelflächen. Eine Zylinderfläche (a) entsteht, wenn durch alle Punkte einer Kurve im Raum eine stetige Folge von Geraden (die Erzeugenden) geht, die parallel zueinander verlaufen. Schneiden sich die Erzeugenden dagegen alle in einem Punkt, beschreiben sie eine Kegelfläche (b). Dass eine beliebige Zylinder- oder Kegelfläche abwickelbar ist, läßt sich leicht einsehen, wenn man sie sich durch ein vielkantiges Prisma beziehungsweise eine vielkantige Pyramide ersetzt denkt und sich die einzelnen ebenen Flächen an den Kanten durch ein Scharnier aneinanderhängend vorstellt. Zwanglos lassen sich diese Gebilde in die Ebene auseinanderklappen.
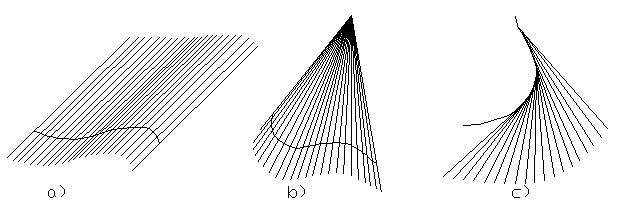
Grundformen der abwickelbaren Flächen: Zylinderfläche, Kegelfläche, Tangentenfläche
Außer der Zylinder- und Kegelfläche ist nur noch die Tangentenfläche (c) abwickelbar. Sie entsteht durch die stetige Folge der Tangenten an eine Raumkurve.
1.2 Die allgemeine abwickelbare Fläche – Kombination aus Zylinder, Kegel und Tangentenfläche
Die allgemeinste abwickelbare Fläche (Developable Surface) besteht aus Stücken von Zylindern, Kegeln und Tangentenflächen, die entlang gemeinsamer Erzeugender glatt aneinandergeheftet sind.
Abwickelbare Fläche (Developable Surface) – Kombination aus Zylinder-, Kegel- und Tangentenfläche
1.3 Regelfläche
Abwickelbare Flächen werden häufig mit den Regelflächen verwechselt. Jede Fläche, die durch die stetige Bewegung einer Geraden im Raum überstrichen wird, ist eine Regelfläche. Die einzelnen Positionen der Geraden sind die Erzeugenden der Fläche.
Die Unterscheidung zwischen abwickelbaren Flächen und Regelflächen ist deswegen wichtig, weil zwar alle abwickelbaren Flächen Regelflächen sind. Aber nicht alle Regelflächen sind zugleich auch abwickelbar.
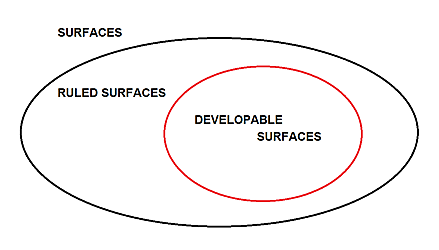
Abwickelbare Flächen sind eine Teilmenge der Regelflächen.
Ein Beispiel für eine Regelfläche, die sich allein durch Verbiegung nicht verebnen läßt, ist die Wendelfläche, die durch die gerade Achse der Blätter einer zweiflügligen Schiffsschraube überstrichen wird, wenn diese sich dreht und vorwärts bewegt. Sie ist eine Regelfläche, die aufeinanderfolgenden Positionen der Blattachse sind die Erzeugenden. Aber sie ist nicht abwickelbar. Ein Blechstreifen läßt sich ohne Dehnung nicht in diese Form bringen.
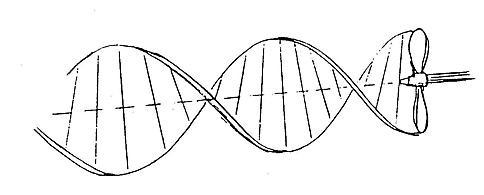
Wendelfläche – Beispiel für eine Regelfläche, die allein durch Verbiegen nicht verebnet werden kann
Regelflächen und abwickelbaren Flächen ist gemeinsam, dass sie durch gerade Erzeugende gebildet werden. Die entscheidende Zusatzforderung dafür, damit eine Regelfläche auch eine abwickelbare Fläche ist, lautet:
Längs einer Erzeugenden muß die Flächennormale die gleiche Richtung haben.
Oder anschaulicher ausgedrückt:
Eine abwickelbare Fläche wird von einer Ebene stets entlang einer Erzeugenden berührt.
Eine Ebene berührt eine abwickelbare Fläche immer entlang einer Erzeugenden.
Die Konservendose liegt vollständig entlang einer Mantellinie auf der Unterlage, ebenso der Kegel. Bei der Wendelfläche verläuft die Flächennormale immer senkrechter zur Propellerwelle, je mehr man sich dieser nähert. Eine Kugel dagegen berührt eine Ebene nur in einem Punkt. Womit anschaulich klar wird, warum ein Boot mit abwickelbarer Außenhaut kein Rundspanter sein kann. Würde man einen Rundspanter auf eine ebene Fläche legen, würde die Außenhaut immer nur an einem oder mehreren einzelnen Punkten berühren, aber nie entlang einer Linie.
Regelfläche in MultiSurf
In MultiSurf wird eine Regelfläche als Ruled Surface zwischen zwei Kurven (Stützkurven) erzeugt, in dem Punkte mit gleichem t-Parameterwert auf beiden Kurven mit Linien (Rulings) verbunden werden. Eine Ruled Surface interpoliert beide Stützkurven, Vorder- und Hinterkante sind gerade.
Regelfläche (Ruled Surface)
In besonderen Fällen ist eine Ruled Surface abwickelbar. Ist zum Beispiel Kurve 2 eine Translationskopie von Kurve 1, dann ist die Ruled Surface ein allgemeiner Zylinder. Ist Kurve 1 oder Kurve 2 ein Punkt, dann ist die Ruled Surface eine allgemeine Kegelfläche mit diesem Punkt als Spitze. Zylinder und Kegel sind immer abwickelbar.
Translationsfläche mit gerader Erzeugender
Eine Translationsfläche (Translation Surface) entsteht, wenn eine erzeugende Kurve entlang einer Leitkurve wandert, ohne dabei zu verdrehen, das heißt, alle Erzeugenden sind parallel zueinander. Ist die erzeugende Kurve gerade, handelt es sich um eine Zylinderfläche. Da Zylinderflächen immer abwickelbar sind, ist eine Translation Surface mit einer Line als erzeugende Kurve eine abwickelbare Fläche.
Mit Translation Surfaces lassen sich auf einfache Weise abwickelbare Flächen für Deck, Aufbauseite, Aufbaufront etc. erzeugen.
2 Die Vorteile abwickelbarer Flächen
Abwickelbare Flächen lassen sich ausschließlich durch Verbiegung in eine Ebene ausbreiten. Beziehungsweise aus ebenem Material in eine räumliche Gestalt „aufwickeln“. Längenänderung der Flächenfasern, also Stauchungen oder Dehnungen, treten dabei nicht auf. Bestehen Außenhaut, Deck und Aufbauten eines Bootes aus abwickelbaren Flächen, ergeben sich folgende Vorteile:
- Verwendung von Plattenmaterial. Rumpfschale, Deck, Aufbauten können vollständig aus ebenen Platten gefertigt werden (Stahl, Alu, Sperrholz, GfK-Sandwich). Da Plattenmaterial in großer Länge geliefert wird, ergeben sich weniger Stöße.
- Keine besonderen Fertigungsmöglichkeiten erforderlich. Platten lassen sich leichter biegen als dehnen oder stauchen, so dass selbst große metallene Rümpfe sich noch mit Handwerkzeugen bauen lassen, während sonst Presswerkzeuge erforderlich sind, um die Außenhautplatten durch plastische Verformung in die richtige Gestalt zu bringen. Daher für den Amateurbootsbau sehr geeignet.
- Kein Anpassen. Die verebnete Form der Außenhautplatten läßt sich genau vorausbestimmmen; paßgenau können Schotte, Spanten, Stringer, Längsträger, etc. vorgefertigt werden.
- Der Aufwand für den Bauhelgen reduziert sich auf ein Mindestmaß. Ein einfaches Gestell reicht aus, um die einzelnen Aussenhautplatten in der richtigen Lage zueinander zuhalten. Durch Zusammenheften der Plattenkanten ergibt sich die Rumpfform automatisch.
- Kurze Bauzeit. Gegenüber einem gleichgroßen Rundspanter ergeben sich durchschnittlich Zeiteinsparungen für den Schalenbau von 50%.
- Glatte Außenhaut. Zuerst können die Außenhautplatten zusammengefügt werden, anschließend lassen sich Spanten, Schotte etc. einsetzen, was besonders bei Metallrümpfen die Neigung zur Bildung von Beulen vermindert.
Alle Vorteile zusammengefaßt: der Bau von Booten mit abwickelbaren Flächen ist einfach und kostengünstig.
3 Abwickelbare Flächen mit MultiSurf
3.1 Developable Surface
Der Flächentyp „abwickelbare Fläche“ heißt in MultiSurf Developable Surface. Ihre Eltern sind zwei Kurven im Raum (Stützkurven). Eine Developable Surface wird auf folgende Weise erzeugt:
Bestimmung der Erzeugenden
Zunächst wird auf Kurve 1 ein Punkt A gewählt und zu diesem auf Kurve 2 ein Punkt B gesucht, derart, dass eine Ebene beide Kurven in diesen Punkten gleichzeitig berührt. Die Verbindungslinie AB ist dann eine Erzeugende (Ruling) der abwickelbaren Fläche. Nun wird ein neuer Punkt A auf Kurve 1 gewählt und dazu auf Kurve 2 wiederum der entsprechende Punkt B gesucht. Man kann sich dieses Verfahren anschaulich so vorstellen, dass an die beiden Kurven eine materielle Ebene gelegt und weitergewälzt wird. Die Erzeugenden sind gleichzeitig auch die Biegelinien, entlang denen die Fläche bei der Verebnung beziehungsweise beim Gegenteil, der "Aufwicklung" der ebenen Fläche, verbogen wird.
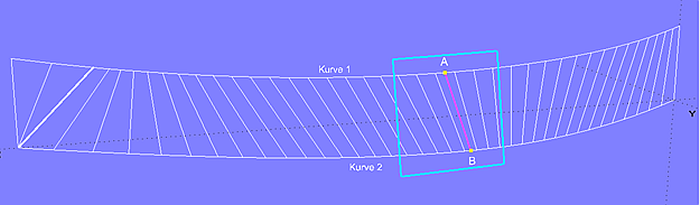
Berührungsebene – Erzeugung der Rulings der abwickelbaren Fläche
Das vorstehend beschriebene Verfahren wird solange fortgeführt, bis Rulings zwischen Anfang und Ende beider Kurven gefunden wurden. Ist auf einer Kurve das Ende erreicht, aber auf der anderen Kurve noch nicht, verlaufen die restlichen Rulings strahlenförmig (Kegelfläche). Im vorstehenden Bespiel ist dies am linken Ende von Kurve 2 der Fall.
Verlaufen Rulings (Erzeugende) parallel zueinander, ist in diesem Bereich die Fläche zylinderförmig; verlaufen sie aufgefächert, ist sie Teil einer Tangentenfläche; haben auf einer Kurve Rulings den gleichen Endpunkt, ist sie Teil einer Kegelfläche.
Es ist wichtig, dass beide Stützkurven die gleiche Orientierung haben. Die Kante u = 0 einer Developable Surface ist ein Ruling, der den Anfang von Kurve 1 mit dem Anfang von Kurve 2 verbindet, die Kante u = 1 verbindet die beiden Kurvenenden. Ist die Orientierung der Stützkurven gegenläufig, muß mit einer SubCurve oder SubSnake die Orientierung einer der beiden Kurven umgedreht werden.
Breaklines
Wird in einer Developable Surface ein Ruling auf dem Bildschirm mit etwas größerer Strichstärke dargestellt als die anderen, ist dies eine sogenannte Breakline. Sie kennzeichnet eine Stelle, wo Rulings den gleichen Endpunkt haben, also strahlenförmig verlaufen.
Breaklines in einer abwickelbaren Fläche sind ein Hinweis, hier genauer hinzusehen. Es kann Probleme geben, muß es aber nicht.
Zum einen können bei strahlenförmig verlaufende Rulings in diesem Bereich Schnitte durch die Fläche nicht gut straken. Dazu im Nachfolgenden mehr.
Zum anderen können bei auftretenden Breaklines weitere Konstruktionen, die von den geometrischen Eigenschaften der Fläche abhängen, eine Fehlermeldung verursachen. Zum Beispiel bei einem Rolling Ball Fillet, einer Sweep Surface oder einer Tangent Boundary Surface. Dadurch, dass Rulings strahlenförmig verlaufen, also den gleichen Endpunkt haben, können an einer solchen Stelle geometrische Größen wie beispielsweise die Richtung der Tangente an der Flächenkante nicht berechnet werden (der Abstand zwischen Punkten ist gleich Null).
Die Anordnung der Erzeugenden und ihr Einfluß auf den Strak
Eine Developable Surface ist nicht automatisch eine glatte Fläche. Man nehme ein Blatt Papier und falte es beliebig zusammen. Es ist und bleibt eine abwickelbare Fläche.
Auch wenn beide Stützkurven harmonisch verlaufen, können Unregelmäßigkeiten im Strak der Fläche auftreten. Der Verlauf der Rulings gibt hierfür eindeutige Hinweise.
Modell 2triangles_a.ms2 enthält eine abwickelbare Fläche zwischen zwei windschiefen Linien. Im Längsschnitt ist deutlich ein Knick in der Fläche zu sehen. Der Verlauf der Rulings zeigt, dass die Fläche aus zwei dreieckförmigen, ebenen Teilstücken besteht.
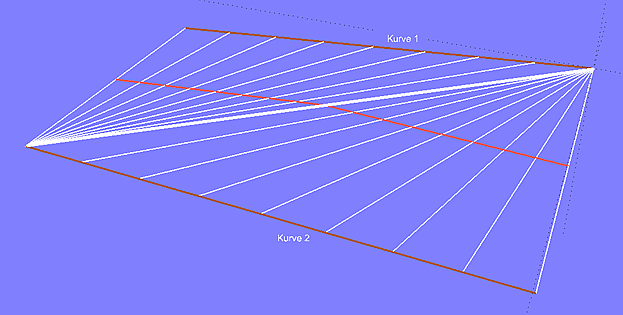
Modell 2triangles_a.ms2 - abwickelbare Fläche zwischen zwei windschiefen Linien
Während Punkt A entlang Kurve 1 fortschreitet, stagniert Punkt B auf Kurve 2. Erst wenn Punkt A das Kurvenende erreicht hat, wandert Punkt B auf Kurve 2, wobei Punkt A nun seinerseits stagniert.
Immer wenn Ruling-Endpunkte nicht fortschreiten, sondern stagnieren, oder sich die Richtung umkehrt, in der sie fortschreiten, kann dies sich negativ auf die Form der Fläche auswirken. Ist der Rulingsverlauf aber harmonisch, sind Schnitte durch die Fläche regelmäßig.
Die Anordnung der Rulings hängt einzig und allein vom Verlauf der beiden Stützkurven zueinander ab. Ist die Fläche nicht glatt, muß man die Form einer Kurve oder auch beider Kurven ändern.
Der Typ der Stützkurve spielt bei einer Developable Surface keine Rolle. Zum Beispiel kann man bei der Bodenfläche eines Rumpfes als Knickkurve eine C-spline Curve verwenden, und die Bodenkontur einschließlich Vorfuß mit einer B-spline Curve formen.
Im Gegensatz zu Flächenarten wie den Lofted Surfaces hat es auf den Verlauf der Rulings auch keinen Einfluß, welche Parameterverteilung und wieviele Kontrollpunkte (Cps) die Stützkurven haben. Wegen der Art und Weise, wie eine abwickelbare Fläche erzeugt wird (Abwälzen einer Ebene), kommt es ausschließlich auf den relativen Verlauf der Kurven zueinander an.
Die Erzeugenden einer abwickelbaren Fläche sind ein Scharnier, um die angrenzende Flächenteile verdreht beziehungsweise verbogen werden. Die Biegung der Fläche ist quer zur Richtung der Rulings (Biegelinien, Wälzlinien). Verlaufen Rulings in Spantrichtung, sind Spanten gerade. Verlaufen sie schräg in der Fläche, sind Spanten konvex. Je schräger die Rulings, umso konvexer die Spanten. Man kann die Form von Spanten, Schnitten, Wasserlinien durch eine Developable Surface nur über die Anordnung der Rulings beeinflussen, also über die Stützkurven und deren Verlauf zueinander.
Stark gekrümmter Spant im Vorschiff aufgrund schräg verlaufender Rulings
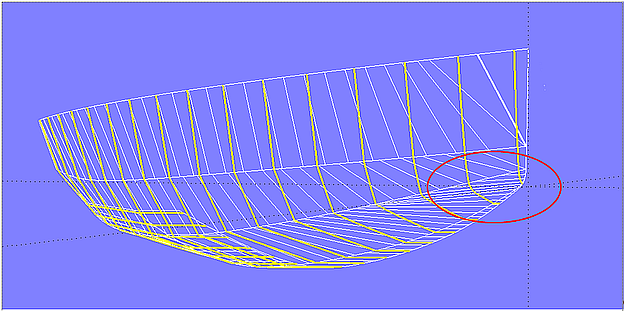
Ersetzt man im Modell 2triangles_a.ms2 die Developable Surface durch eine Ruled Surface, erhält man ein völlig anderes Bild (Modell 2triangles_b.ms2). Es gibt keine Breakline.
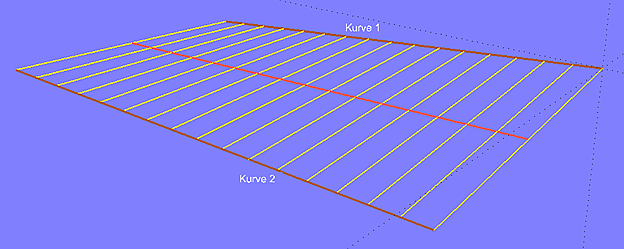
Modell 2triangles_b.ms2 – Ruled Surface zwischen zwei windschiefen Linien
Beiden Flächenarten sind die geraden Erzeugenden gemeinsam, aber das Verfahren, wie diese bestimmt werden, ist ganz unterschiedlich. Darum ist es keine gute Idee, eine Developable Surface durch eine Ruled Surface zu ersetzen, um eine harmonische Anordnung der Rulings zu erhalten. Die Abwickelbarkeit geht verloren.
Es ist immer zu beachten, dass Abwickelbarkeit eine Einschränkung der Formgebung bedeutet. Die zwischen ihren beiden Stützkurven aufgespannte Developable Surface hat ihre eigenen Gesetzmäßigkeiten, an die sich der Konstrukteur mit seinen Formwünschen anpassen muß.
3.2 Straken von Developable Surfaces
Dass abwickelbare Flächen nicht automatisch glatte Flächen sind, wurde bereits erwähnt. Ebenso, dass die Anordnung der Rulings nur davon abhängt, wie ihre beiden Stützkurven relativ zueinander verlaufen.
Allgemeine Hinweise
- Man muß versuchen, den Rulingverlauf harmonisch zu machen. Stehen zum Beispiel in der Mitte einer Developable Surface die Rulings mehr oder weniger senkrecht, um sich dann nach achtern zu neigen und abschließend am Flächenende wieder senkrecht zu werden, so bedeutet dies für die Spanten: in der Mitte keine Krümmung, dann zunehmende, dann wieder abnehmende Krümmung. Bei einem Rundspantrumpf würde man eine derartige Spantentwicklung nicht akzeptieren. Durch Ändern der Stützkurven sollte versucht werden, dass sich die Rulingneigung bis achtern fortsetzt.
- Man muß ausprobieren, auf welche der beiden Kurven die Rulings am ehesten in der gewünschten Weise reagieren.
- Immer dann, wenn eine Abfolge von Spanten nicht parallel verläuft, sondern sie sich zunehmend verdrehen, entstehen durch die schräg in der Fläche verlaufende Rulings stark gekrümmte Spanten. Abhilfe schafft nur die Verringerung der Verwindung der Spanten.
- Ein Steven mit stark gekrümmtem Vorfuß macht mehr Probleme hinsichtlich harmonischer Spanten als ein sanfter Übergang zwischen Bodenkontur und Vorsteven.
- Schmale Aussenhautplatten mit starker Spantkrümmung müssen bei Metallrümpfen maschinell vorgebogen werden. Platten aus Sperrholz oder GfK-Sandwich müssen in Richtung der Biegelinien eingeschnitten werden, damit sie weniger biegesteif sind.
Im Folgenden werden Methoden gezeigt, wie sich die Form abwickelbarer Flächen in Grenzen beeinflussen läßt. Als Beispiel wird die Bodenfläche eines Motorbootes gewählt, aufgespannt zwischen der Knickkurve (chine) und der Bodenkontur (keel). Da diese Kurven besonders im Heckbereich wenig gekrümmt verlaufen, kann der Verlauf der Rulings (Erzeugende, Wälzlinien, Biegelinien) hier unregelmäßig sein.
Strahlenförmiger Verlauf der Erzeugenden
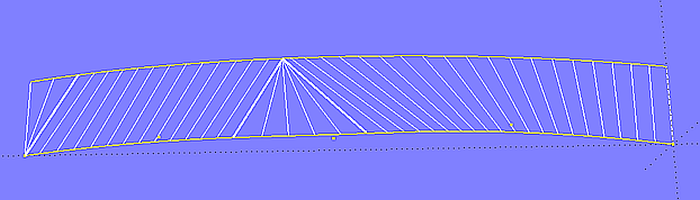
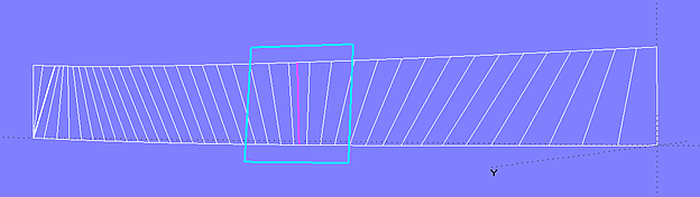
Enden beide Kurven an der gleichen X-Position, laufen Rulings häufig strahlenförmig zum Ende einer der beiden Kurven. Im Modell bottom_panel-1.ms2 ist ersichtlich, dass dieser Rulingverlauf eine unharmonische Krümmung der achterlichen Spanten verursacht.
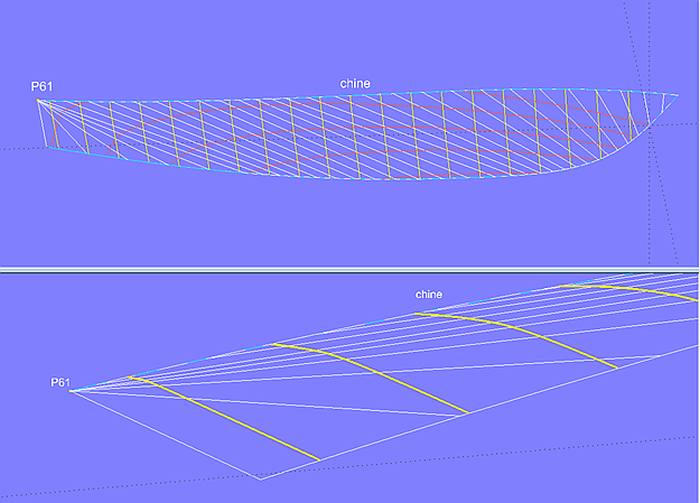
Modell bottom_panel-1.ms2 - Bodenfläche eines Motorbootes. Die Rulings laufen achtern strahlenförmig zum Ende der Kurve chine.
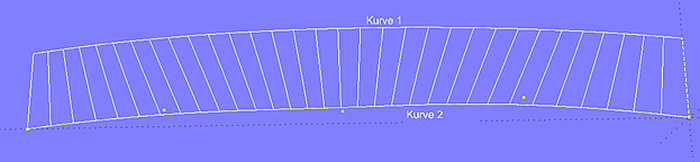
Hebt man den Punkt P61 etwas an, verlaufen die Rulings parallel zur Hinterkante und der Spantverlauf wird gleichmäßiger.
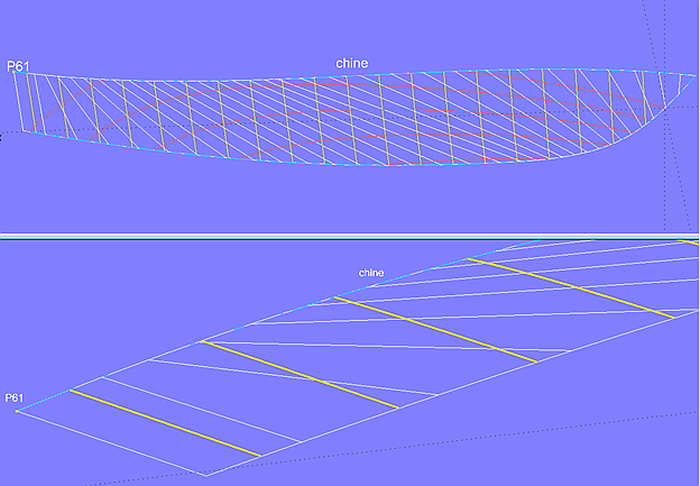
Modell bottom_panel-2.ms2 – durch Anheben des Punktes P61 erhält die Kurve chine etwas mehr Krümmung, was sich günstig auf den Rulingverlauf und damit auf die Spantform auswirkt.
Hinterkante mit Bucht
Sollen Spanten bis zum Heck gekrümmt sein, muß man verhindern, dass die Rulings strahlenförmig enden. Dazu gibt es mehrere Möglichkeiten.
Methode 1 – längere Stützkurve
Eine Möglichkeit, dies zu erreichen, zeigt Modell bottom_panel-3.ms2. Die Kurve chine endet nicht am Heck, sondern geht etwas darüber hinaus.

Modell bottom_panel-3.ms2 – die Kurve chine endet hinter dem Spiegel. Dadurch verlaufen die Rulings aufgefächert.
Methode 2 - SubCurve
Eine weitere Möglichkeit zeigt Modell bottom_panel-4.ms2. Beide Kurven enden am Heck, aber Kurve chine wird über eine SubCurve verlängert. Zunächst erzeugt man zwei Beads, einen am Kurvenanfang und einen am Kurvenende (e1), damit dann eine SubCurve (extended_chine). Da in MultiSurf Kurven auch jenseits des nominellen Parameterbereichs zwischen t = 0 und t = 1 definiert sind, erhält man eine Verlängerung der Kurve, wenn e1 über das Kurvenende hinaus verschoben wird (t > 1). Diese Methode ist häufig ausreichend, um den Rulingverlauf wie gewünscht zu ändern.
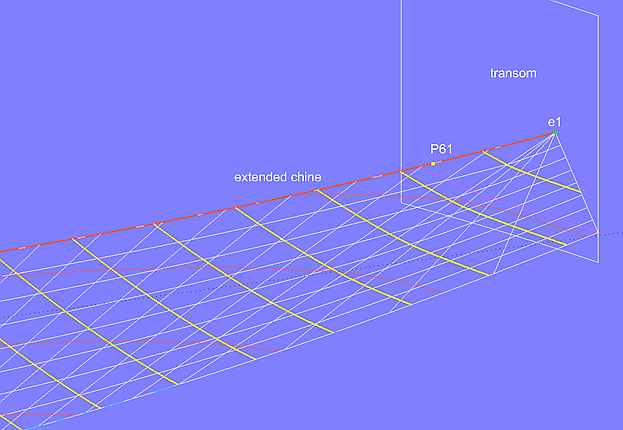
Modell bottom_panel-4.ms2 – Verlängerung der Knickkurve mit einer SubCurve (Ansicht schräg von oben vorn)
Methode 3 – zusammengesetzte Stützkurve
Es ist nicht erforderlich, dass die Stützkurven einer abwickelbaren Rumpffläche nur in Längsrichtung verlaufen. Wie in Modell bottom_panel_5.ms2 gezeigt, kann man sie auch aus Teilstücken so zusammensetzen, dass sie die Hinterkante der Fläche miteinschließt. Auf diese Weise kann die Spantkrümmung in diesem Bereich kontrolliert werden.
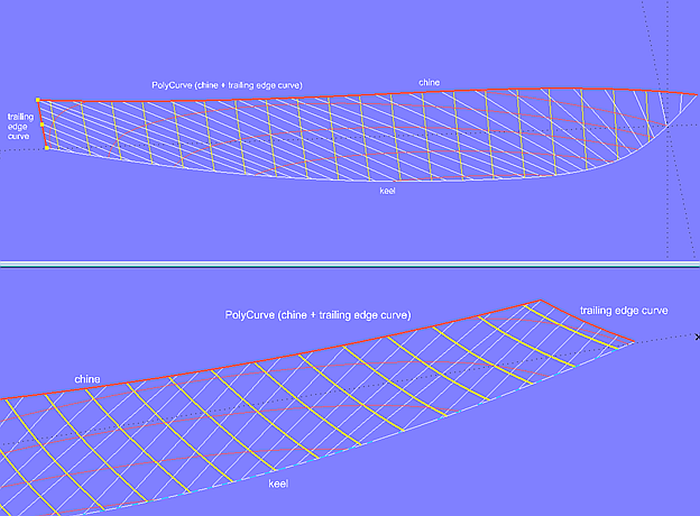
Modell bottom_panel-5.ms2 – Stützkurve als PolyCurve (zusammengesetzt aus Knick und Kurve der Hinterkante)
Teilweise gerader Verlauf einer Stützkurve
Wenn eine der Stützkurven der abwickelbaren Fläche gerade verläuft, berührt die abwälzende Ebene dann komplett entlang dem geraden Kurvenstück, und nicht nur in einem Punkt. Auch in diesem Fall entstehen strahlenförmig angeordnete Rulings, was zu unregelmäßigem Strak führen kann. Modell bottom_panel-6.ms2 zeigt ein Beispiel. Die Bodenkontur ist eine B-spline Curve, Degree-3; ihre Cps 5, 6 und 7 liegen auf einer Linie, ab cp5 verläuft die Bodenkontur gerade.
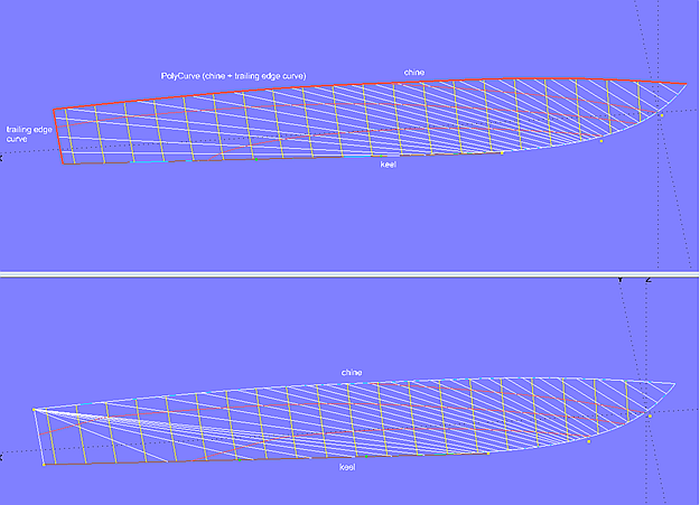
Modell bottom_panel-6.ms2 – die Bodenkontur (keel) verläuft achtern gerade. Durch Zusammenfügen von Knick und Hinterkante wird die Anordnung der Rulings regelmäßiger.
Durch Zusammenfügen von Knick und Hinterkante läßt sich eine regelmäßige Anordnung der Rulings erreichen. Und damit strakende Schnittkurven durch die abwickelbare Fläche (Spanten, Wasserlinien etc.).
Stützkurve mit Wendepunkt
Soll eine der beiden Stützkurven einer abwickelbaren Fläche einen Wendepunkt (S-Schlag) haben, wie es z. B. bei der Bodenkontur eines Motorbootes aus konstruktiven Gründen erforderlich sein kann, zeigen sich im allgemeinen Unregelmäßigkeiten im Verlauf der Rulings - und daraus resultierend unharmonische Wasserlinien, Spanten, Schnitte. Modell bottom_panel-7a.ms2 ist exemplarisch hierfür.
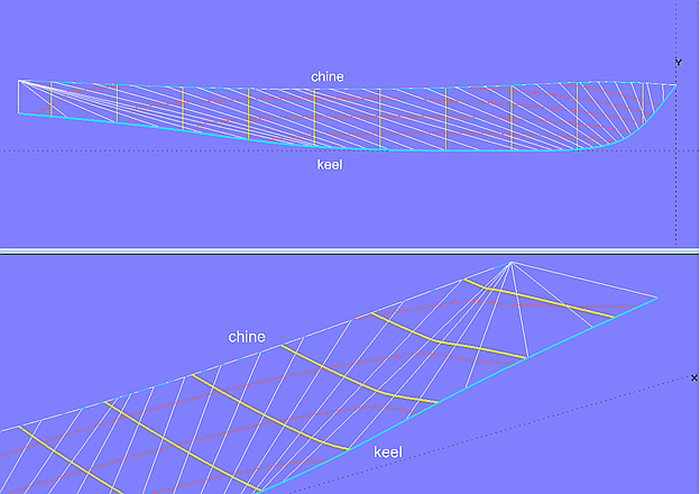
Modell bottom_panel-7a.ms2 – durch den Wendepunkt der Kurve keel verlaufen die Rulings nicht gleichförmig - Spanten straken nicht.
Abhilfe kann in einem solchen Fall nur die Aufteilung in zwei Teilflächen schaffen. Die vordere Fläche in Modell bottom_panel-7b.ms2 ist abwickelbar (Developable Surface), die hintere Fläche ist eine Ruled Surface. Meistens muß diese beim Bau nur geringfügig plastisch verformt werden
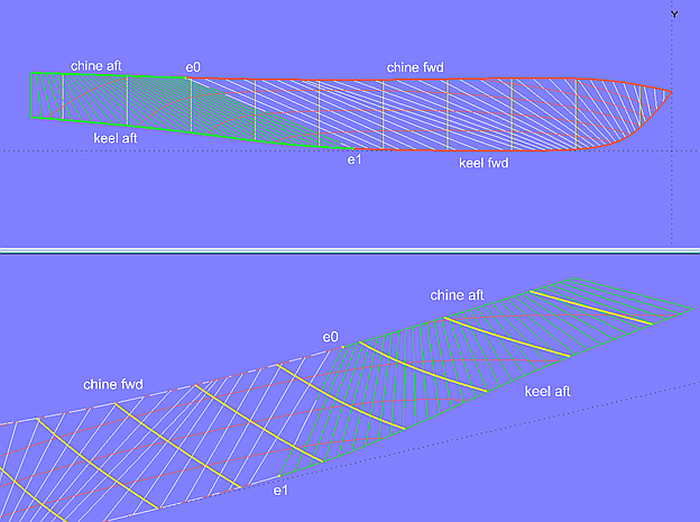
Modell bottom_panel_7a.ms2 – Bodenfläche aufgeteilt in zwei Teile. Bugteil ist abwickelbar (Developable Surface), Heckteil ist eine Ruled Surface, die plastische Verformung erfordert.
4 Rumpfentwurf mit abwickelbaren Flächen
Ein Boot mit abwickelbarer Außenhaut kann nur ein Knickspanter sein. Plattboden, Skiff, Scharpie, Multiknick sind Beispiele für Knickspantformen bei Segelyachten, bei Motorbooten ist die V-Form weit verbreitet. Im Folgenden wird gezeigt, wie sich typische Rumpfformen mit abwickelbaren Flächen entwerfen lassen.
4.1 Moderner Knickspanter
Modell sy15_double_chine.ms2 ist die Knickspantversion des im Tutorium „Rundspantrumpf mit durchlaufendem Knick“ beschriebenen Modells sy15_full_chine.ms2. Den Rumpfbereich unterhalb der Seitenfläche bilden 3 Developable Surfaces. Die untere Stützkurve der Kimmfläche chine_strake_2 ist eine B-spline Curve mit 8 Cps; sie schließt die Vorfußrundung mit ein. Im Bugbereich sind in dieser Fläche die Spanten stark gekrümmt, bedingt durch die schräg verlaufenden Rulings. Die Fläche wird ja quer zu den Rulings gebogen, und da diese schräg zur Richtung der Spanten verlaufen, sind diese zwangsläufig konvex.
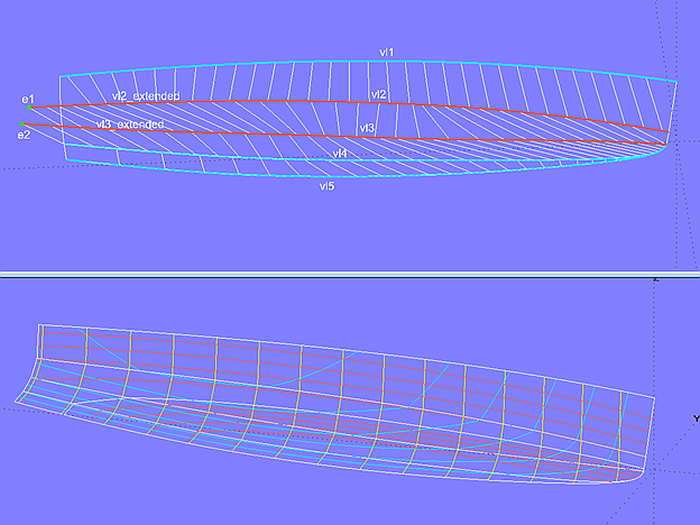
Modell sy15_double_chine.ms2 – moderner Knickspantrumpf. Die oberen Stützkurven der beiden Kimmflächen sind jeweils durch SubCurves verlängert, um eine gleichförmige Anordnung der Rulings zu erreichen.
Spantvergleich – Basismodell: sy15_full_chine.ms2; Knickspantversion: sy15_double_chine.ms2
4.2 Klassischer Knickspanter
Modell multi_chine_classic.ms2 zeigt einen Langkielrumpf in Knickspantform. Am Bug gehen die oberen 4 Plattengänge über die Mittschiffsebene hinaus, um die Vorstevenkontur zu runden. Sie ist also indirekt bestimmt.
Die jeweils letzten Kontrollpunkte der Stützkurven sind Magnete auf der Spiegelfläche.
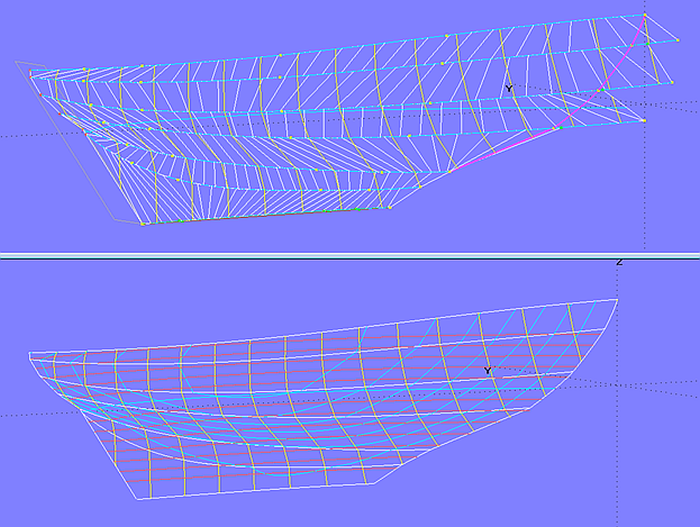
Modell multi_chine_classic.ms2 – Langkiel-Knickspantrumpf
4.3 Motorboot
Den Rumpf eines Motorbootes zeigt Modell cruiser.ms2 (abgeleitet aus einem MultiSurf-Modell von AeroHydro Inc.). Seite, Boden, Bugrundung und Spiegel bestehen aus abwickelbaren Flächen. Für die untere Stützkurve der Seitenfläche (topside) wird die Knickkurve (chine) und der Verlauf der Hinterkante (n1) der PolyCurve polychine1 zusammengefaßt. Ebenso wird für die Bodenfläche (bottom) verfahren, hier bilden die Kurven von Knick (chine) und Hinterkante (n2) die PolyCurve polychine2.
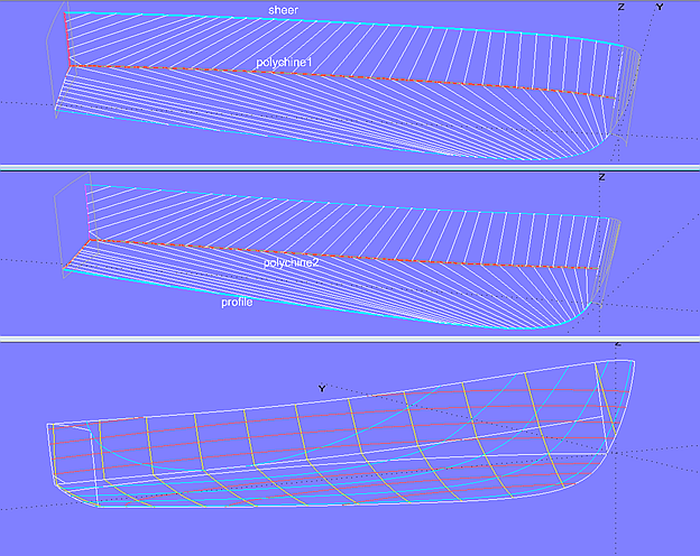
Modell cruiser.ms2 – Stützkurven von Seite und Boden
Die Hinterkanten von Seite und Boden sind B-spline Snakes (n1, n2) auf der Basisfläche des Spiegels (transom_0), so dass kein Trimmen überstehender Teile erforderlich ist.
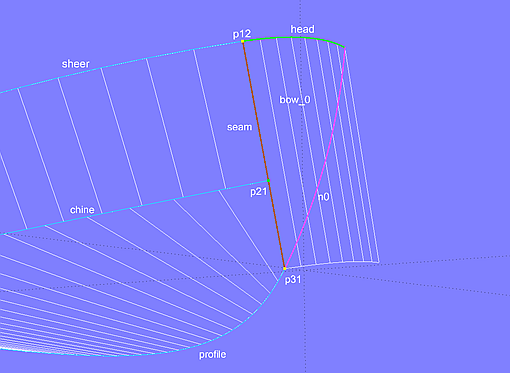
Modell cruiser.ms2 – Konstruktion der Bugrundung
Die Basisfläche der Bugrundung ist die Translation Surface bow_0, erzeugt mit Line seamund B-spline Curve head, der Abrundung der Rumpfoberkante (C-spline Curve sheer). Line seam verläuft zwischen dem ersten Cp (p11) der Rumpfoberkante und dem ersten Cp (p31) der Bodenkontur (B-spline Curve profile). Der erste Cp der Knickkurve (chine) ist ein Bead (p21) auf Line seam, so dass Seite und Boden entlang der Linie und tangential zur Translation Surface bow_0 beginnen.
5 Besondere Rumpfformen
5.1 "Radius Chine" - Rumpf
Möchte man einerseits die Fertigungsvorteile von abwickelbaren Knickspantrümpfen nutzen, andererseits Nachteile durch erhöhten Widerstand vermeiden, bietet sich die "Radius Chine“-Rumpfform an. Zunächst entwirft man einen einfachen Knickspantrumpf mit zwei abwickelbaren Flächen für Rumpfseite und Rumpfboden. Dann wird der Kimmbereich durch eine Fläche abgerundet.
Methode 1
Im Modell radius_chine-1.ms2 ist die Abrundung eine C-spline Lofted Surface mit 4 B-spline-Mcs. Da eine B-spline Curve tangential zur Linie zwischen ihrem 1. und 2. Cp beginnt und tangential zur Linie zwischen ihrem vorletzten und letzten Cp endet, wird der glatte Anschluß an Seite und Boden fest eingebaut, in dem man für Cp1 und Cp3 einen Bead auf der Linie zwischen Deck und Kimm beziehungsweise zwischen Kimm und Boden verwendet. Beispiel: die Cps für mc2 sind Bead e21, Point p22 und Bead e22. Bead e21 liegt auf der Line l2 zwischen p21 und p22, also beginnt mc2 tangential zu dieser. Bead e22 liegt auf der Line l3 zwischen p22 und p32, also endet mc2 tangential zu l3.
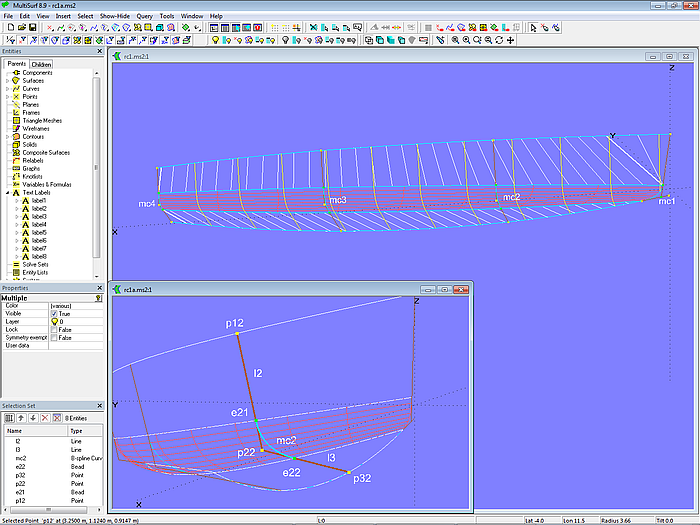
Modell radius_chine-1.ms2 – Abrundung zwischen den abwickelbaren Flächen von Seite und Boden durch eine C-spline Lofted Surface. Der tangentiale Anschluß der Mcs ist fest eingebaut, z. B. bei mc2 durch Bead e21 auf Line l2 und Bead e22 auf Line l3.
Methode 2
Modell radius_chine-2.ms2 ist ähnlich aufgebaut wie radius_chine-1.ms2, aber für mc2, mc3 und mc4 wird keine B-spline Curve verwendet, sondern die Kurvenart Radius Arc. Beispiel mc2: der Kreisbogen startet tangential zur Line l2 zwischen den Punkten p12 und p22 und endet tangential zur Line l3 zwischen den Punkten p22 und p23.
Auf diese Weise kann man direkt die Größe der Ausrundungsradien vorgeben.
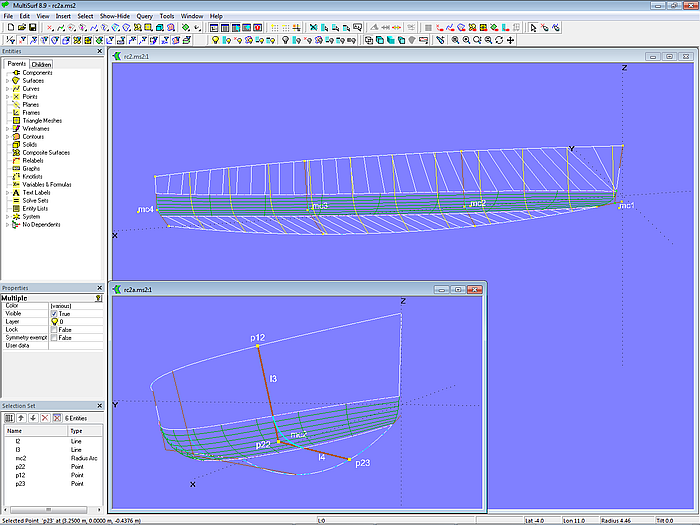
Modell radius_chine-2.ms2 – Masterkurven vom Typ Radius Arc ermöglichen die direkte Vorgabe der Größe der Rundungsradien.
Methode 3
Im Modell radius_chine-3a.ms2 wird die Bilgerundung durch eine Fläche vom Typ Rolling Ball Fillet gebildet. Wie der Name andeutet, kann man sich diese Flächenart entstanden denken durch eine Kugel, die zwischen beiden Flächen abrollt und dabei eine Abrundung überstreicht, die sich zwischen dem Pfad aller Berührpunkte auf der einen Fläche und dem Pfad aller Berührpunkte auf der anderen Fläche erstreckt.
Damit im Vorschiff die Kugel berühren kann, muß der Boden sich über Mitte Schiff hinaus erstrecken; darum verläuft ihre untere Kontrollkurve auf der negativen Seite der Mittschiffsebene. Auch die Seite muß vorne etwas überstehen. Steven, Bodenkontur und Übergang ergeben sich also als Schnitt dieser Basisflächen mit der Mittschiffsebene (*Y = 0).
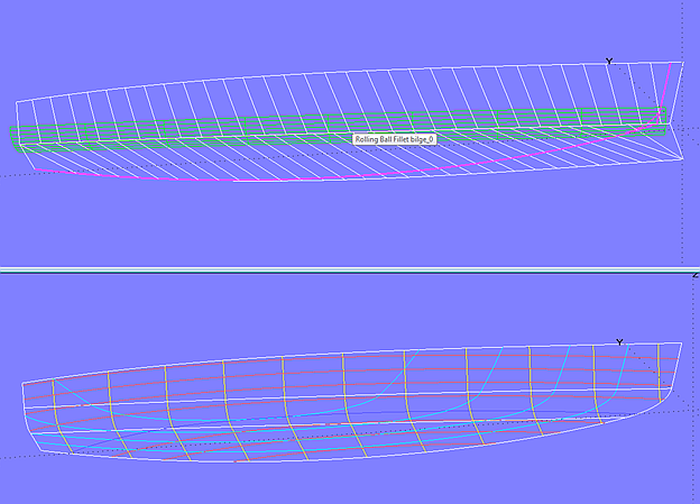
Modell radius_chine-3a.ms2 – Abrundung zwischen Seite und Boden durch Rolling Ball Fillet (Radius konstant)
Beim Rolling Ball Fillet kann der Radius der rollenden Kugel mit Hilfe eines Graph-Objektes verändert werden. Dies ist in Modell radius_chine-3b.ms2 gezeigt. Durch den Graph h0 ist der Radius des Rolling Ball Fillets bilge_0 am Bug halb so groß und mittschiffs doppelt so groß wie am Heck.
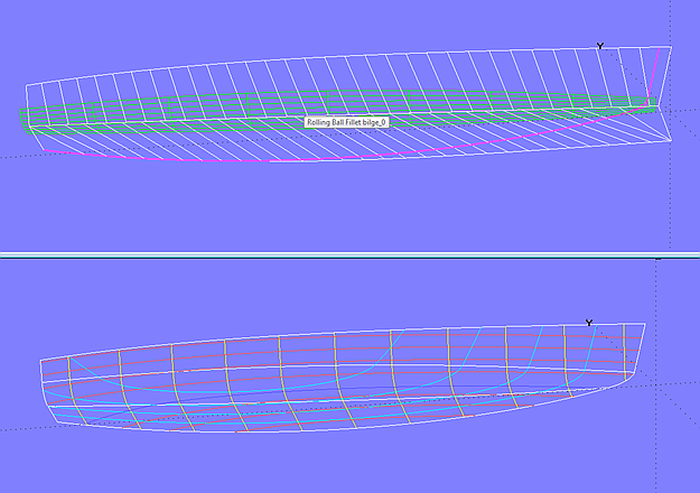
Modell radius_chine-3b.ms2 – Abrundung zwischen Seite und Boden durch Rolling Ball Fillet (Radius variabel)
Welche Methode für die Rundung der Bilge bei einem Rumpf vom Typ “Radius Chine” verwendet wird, hängt von den Randbedingungen ab. Bei Methode 1 kann die Abrundung frei geformt werden, zum Beispiel parabelförmig, bei Methode 2 ist die Rundung immer ein Kreisbogen, die Zahlenwerte der Radien müssen sich harmonisch ändern. Bei Methode 3 ist die Abrundung kreisbogenförmig mit konstantem oder variablem Radius, aber Vorsteven und Bodenverlauf ergeben sich indirekt; es ist nur ein einziges Objekt für die Abrundung erforderlich.
5.2 Rumpf mit nichtabwickelbarer Teilfläche
Abwickelbarkeit bedeutet eine Einschränkung in der Formgebung. Die innere Gestalt der Fläche kann nur in engen Grenzen beeinflußt werden (über den Verlauf der Rulings). Mit einer abwickelbaren Fläche ist es zum Beispiel nicht möglich, ausfallende Spanten im Vorschiff zu entwerfen. Will man darauf nicht verzichten, muß der betreffende Rumpfbereich mit einer anderen Flächenart erzeugt werden. Modell hardchine_powerboat.ms2 zeigt das Prinzip.
Zunächst werden die beteiligten Stützkurven (hier sheer und chine1) in jeweils zwei Teilkurven unterteilt. Mit den SubCurves sheer_aft und chine1_aft wird die Developable Surface topside_aft definiert. An deren Vorderkante liegt die EdgeSnake n0. Mit den SubCurves sheer_fwd, chine1_fwd, n0 und der Bugkurve stem als Randkurven wird nun die Tangent Boundary Surface topside_fwd erzeugt (mit Tangentenstetigkeit entlang n0). Falls erforderlich kann ihre Form über innere Kontrollpunkte beeinflußt werden.
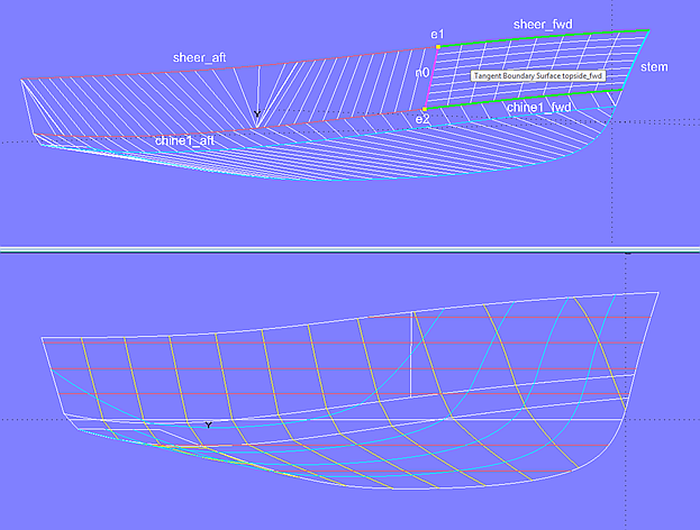
Modell hardchine_powerboat.ms2 – die Teilfläche im Bugbereich ist nicht abwickelbar.
5.3 Rumpf als Kegelfläche
Man erhält immer eine in sich strakende abwickelbare Fläche, wenn sie ausschließlich eine Zylinderfläche, eine Kegelfläche oder eine Tangentenfläche ist. Mitunter soll ein Knickspantrumpf nur durch Kegelflächen gebildet werden. Modell conic_bottom.ms2 zeigt dies am Beispiel einer Bodenfläche. Der Knickverlauf und die Kegelspitze können bei diesem Verfahren vorgegeben werden. Jedoch ist die Mittschiffskontur nicht frei wählbar, sondern ergibt sich als Schnitt der Kegelfläche mit der Mittschiffsebene. Die Rumpfform ist also Einschränkungen unterworfen.
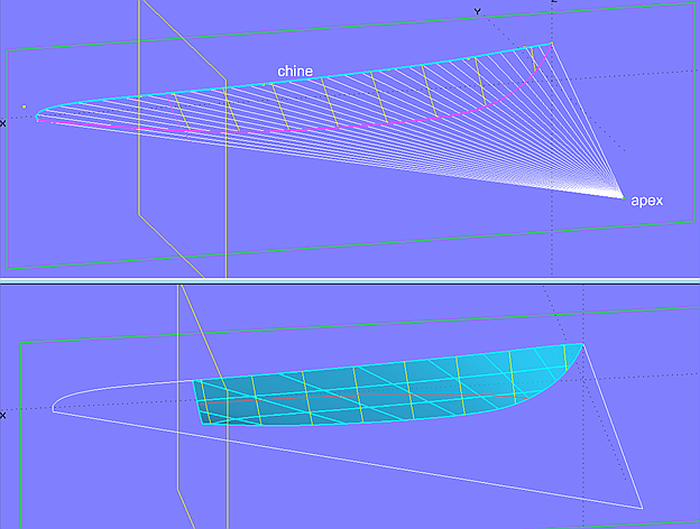
Modell conic_bottom.ms2 – Beispiel einer Bodenfläche als Teil eines Kegels. Die Bodenkontur ergibt sich indirekt als Schnitt mit der Mittschiffsebene.
6 Deck mit abwickelbarer Fläche
Übliche Deckdefinitionen ergeben im Allgemeinen Flächen, die nicht abwickelbar sind. Obwohl Aufbau und Cockpit große Bereiche ausschneiden, was die Problematik der notwendigen Verformung mindert, lassen sich Decks auch als abwickelbare Flächen gestalten.
Eine Möglichkeit, ein abwickelbares Deck zu erzeugen, wird in Modell deck_devsurf.ms2 gezeigt. Die Developable Surface deck_0 wird aufgespannt zwischen der Oberkante des Rumpfes (EdgeSnake n0) und einem Decksbalken am Heck (Arc db).
Der Preis für die einfachere Fertigung einer abwickelbaren Fläche (nur Verbiegung) ist die Einschränkung in der Form. Die Deckskurve auf MS ist gerade, Spanten durch das Deck verlaufen teilweise auch gerade.
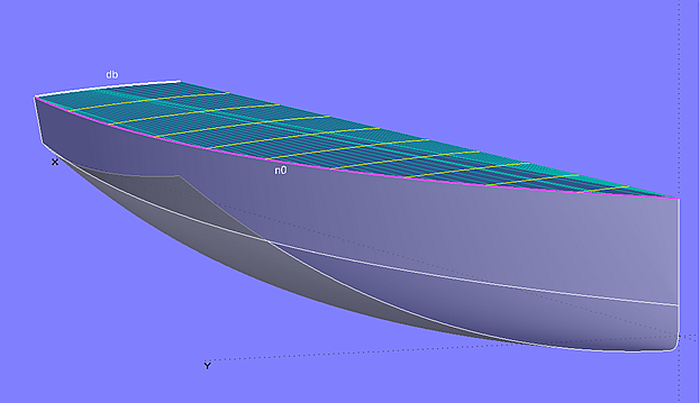
Modell deck_devsurf-1.ms2 – abwickelbare Fläche aufgespannt zwischen Oberkante Rumpf n0 und Deckbalken db achtern
Eine andere Möglichkeit ist die Verwendung einer Kreiszylinderfläche für das Deck. Hat der Verlauf der Rumpfoberkante Priorität, muß das Deck etwas tiefer gelegt werden, so dass ein niedriges Schanzkleid oder eine Fußreling entsteht. Das ist in Modell deck_devsurf-2.ms2 gezeigt.
Die Deckfläche ist eine Translation Surface mit Line line1 als Erzeugende und Arc db als Leitkurve. Da die Erzeugenden gerade sind, ist diese Translation Surface abwickelbar. Sie schneidet die Rumpfseite in der Intersection Snake n0.
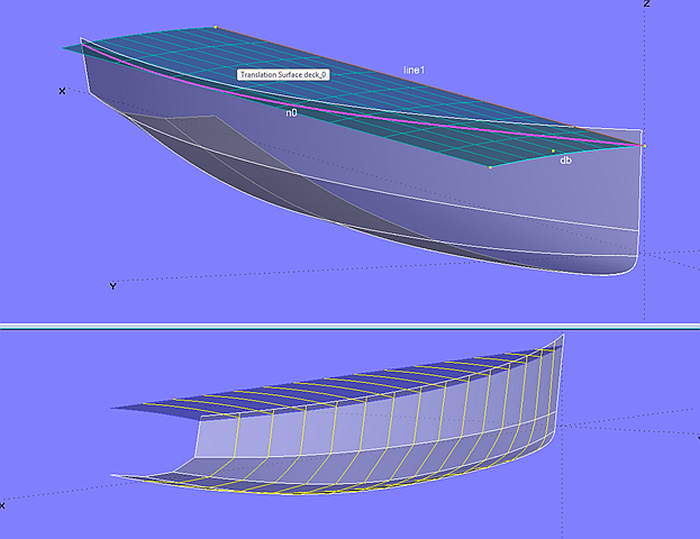
Modell deck_devsurf-2.ms2 – mit line1 und Deckbalken db erzeugte Translation Surface als abwickelbare Fläche
Sollen Oberkante Rumpf und Deckskante zusammenfallen, muß die obere Stützkurve der Rumpfseite in der Decksfläche liegen. Dies ist in Modell deck_devsurf-3.ms2 gezeigt. Die Rumpfoberkante ist also nur eingeschränkt formbar. Bei völligem Verlauf im Vorschiff kann ein Wendepunkt (S-Schlag) entstehen.

Modell deck_devsurf-3.ms2 – die obere Stützkurve der Rumpfseite ist eine C-spline Snake auf der abwickelbaren Decksfläche.
7 Aufbau mit abwickelbaren Flächen
Im Tutorium „Decks und Aufbauten“ gibt es mehrere Beispiele, wie man kastenförmige Aufbauten modellieren kann. Sind deren Flächen vom Typ Translation Surface, wobei die erzeugende Kurve gerade ist, sind sie abwickelbar. Siehe die Modelle trunk_cabin-1.ms2, trunk_cabin-2.ms2, trunk_cabin-3.ms2. Da in diesen Modellen für das Aufbaudach die Leitkurve nicht gerade ist, muß sie durch eine Line ersetzt werden, um auch das Aufbaudach abwickelbar zu machen. Zwar ist dann seine Kontur auf Mitte Schiff nicht mehr gekrümmt, wodurch die Ästhetik leiden mag, aber das ist der Preis für einfache Bauweise.
Modell conic_cabin.ms2<(i> ist ein weiteres Beispiel. Aufbauseitenwand und -frontwand sollen aus einer Fläche gemacht werden. Dafür wird eine allgemeine Kegelfläche verwendet, als Leitkurve dient die Unterkante Aufbau (B-spline Snake auf der Deckfläche). Die Kegelspitze wird entsprechend den gewünschten Neigungen von Seiten- und Frontwand positioniert. Das Aufbaudach ist eine Kreiszylinderfläche. Trimmed Surfaces bilden die fertigen Flächen des Aufbaus.

Modell conic_cabin.ms2 – Aufbauseite und -front als Teil einer Kegelfläche
8 Flächenabwicklung
Alle abwickelbaren Flächen lassen sich mit dem Programm MSDev oder dem MultiSurf-Modul Flattener verebnen und als CAD-Dateien exportieren. Auf der Abwicklung können Markierungen für Biegelinien, Spanten, Wasserlinien etc. angebracht werden.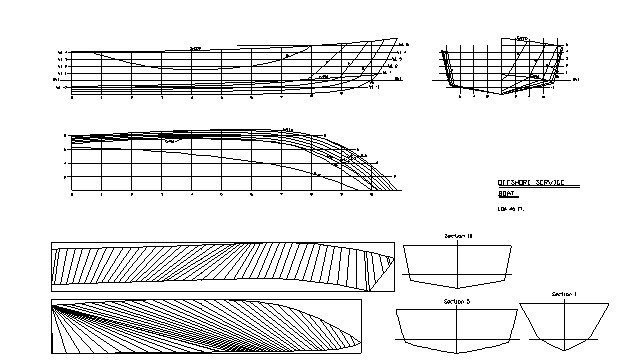
Abgewickelte Rumpfflächen für ein Motorboot
Expanded Surface
Falls MultiSurf mit dem Modul Flattener aktiviert ist, steht auch die Flächenart Expanded Surface zur Verfügung. Damit können in MultiSurf Flächen direkt verebnet werden.

Abwicklung in MultiSurf mit der Flächenart Expanded Surface
Spiegelabwicklung
In bestimmten Fällen läßt sich auch ohne Hilfe durch ein zusätzliches Programm der ebene Umriß einer abwickelbaren Fläche konstruieren. Zum Beispiel für den Spiegel, der bei vielen Booten Teil eines geraden Kreiszylinders ist. Im Modell cyl_transom_expansion.ms2>/i> ist gezeigt, wie man die Abwicklung dieser Spiegelform erhält.
Die Translationsfläche transom_0 ist die Basisfläche des zylinderförmigen Spiegels. Leitkurve ist Arc c1, Erzeugende die Line l1. Die Kontrollpunkte beider Kurven sind im 3-Point Frame F1 definiert, so dass man die Spiegelfläche neigen und verschieben kann, ohne dabei seine Form zu ändern.
Rumpf und Deck werden von der Fläche transom_0 in den Intersection Snakes n1 und n3 geschnitten, die dann ihrerseits als Projected Snakes n2 und n4 auf transom_0 projiziert werden.
Die Abwicklung der Basisfläche des Spiegels ist die Translation Surface s0, deren Leitkurve die Line l2 ist (Endpunkt ist Point pt3), die Erzeugende ist wiederum Line l1. Die Länge der Line l2 muss gleich der Länge des Arc c1 sein. Da s0 in der XZ-Ebene des Frames F1 liegt, entspricht die Z-Koordinate von Point pt3 (Endpunkt von Line l2) einfach der Bogenlänge von c1. Diese Länge wird in Tools/ Mass Properties angezeigt.
Wird der Arc c1 geändert, zum Beispiel um die Spiegelbucht zu vergrößern, muss die Position von pt3 manuell angepasst werden.
Um dies zu vermeiden, wird die einfache Formel f1:
f1 = ARCLEN (c1, 0, 1)
die die Länge von Arc c1 berechnet, für die Z-Koordinate von pt3 verwendet. Auf diese Weise ist es garantiert, dass die Fläche s0 immer so lang ist wie c1.
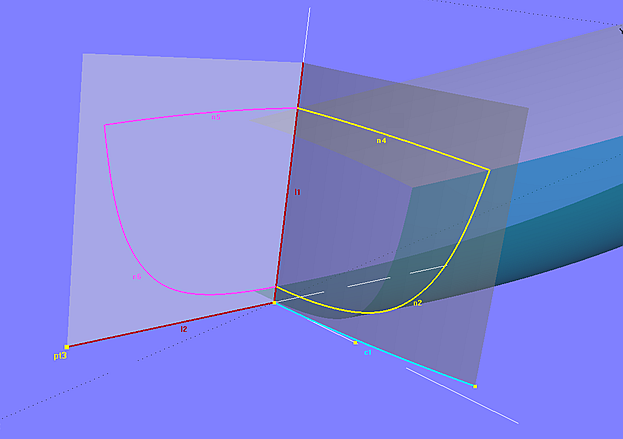
Modell cyl_transom_expansion.ms2 – Konstruktion derSpiegelabwicklung
Um den Umriß des Spiegels auf s0 zu erhalten, werden die beiden Projected Snakes n2 und n4 auf s0 als Copy Snakes übertragen.
Da s0 in der Mittschiffsebene liegt, zeigt die Seitenansicht des Modells (Y-view) auf dem Bildschirm diesen Umriß in wahrer Größe. Alternativ liefert View/ Modify/ Set View/ Normal to... ebenfalls die senkrechte Aufsicht (s0 vorher auswählen). Über File/ Export 2D/ DXF kann diese Ansicht dann exportiert werden.
======================================================================================