Download PDF + Modelldateien

 

Formmerkmale

Über Besonderheiten der Geometrie von Rumpf, Deck und Kiel

von Reinhard Siegel

Juli 2020

 

 

Inhalt

Einleitung

1 Rumpf

• 1.1 - Knick durchlaufend - Segelboot
• 1.2 - Knick auslaufend - Segelboot
• 1.3 - Knick auslaufend – Jolle
• 1.4 - Knick auslaufend - Motorboot
• 1.5 - Gerade Bodenschnitte
• 1.6 - Boden mit Propellertunnel
• 1.7 – Spritzleiste
• 1.8 - Auslaufende Spritzkante
• 1.9 - Fußreling

2 Abrundungen

• 2.1 - Bugrundung
• 2.2 - Deckrundung 1
• 2.3 - Deckrundung 2
• 2.4 - Abgerundete Aufbaukanten
• 2.5 - Abrundung Randbogen Kielflosse
• 2.5 - Ausrundung Kielflosse-Ballast

 

 

Einleitung

Formmerkmale sind spezielle Eigenschaften der Geometrie, die aus Sicht des Konstrukteurs für das Funktionieren seines Entwurfs erforderlich sind. Zum Beispiel ein durchlaufender Knick im Rumpf, ein Tunnel im Boden, eine charakteristische Decksabrundung. Im Folgenden werden Methoden beschrieben, wie sich häufig geforderte Formeigenschaften von Rumpf, Deck und Kiel modellieren lassen. Manche Konstruktionen wurden bereits in vorangehenden Tutorien behandelt. Sie werden hier dennoch angeführt, um eine zusammenfassende Sammlung zu schaffen.

 

Verwendete Abkürzungen:

Cp: Kontrollpunkt, Stützpunkt (control point, support point); synonym verwendet
Mc: Masterkurve, Stützkurve (master curve, support curve); synonym verwendet

cp1, cp2, ...: bezeichnet den 1., 2. ... Punkt in der Liste der Kontrollpunkte einer Kurve. Es ist kein Objektname.
mc1, mc2, ...: bezeichnet die 1., 2. ... Kurve in der Liste der Stützkurven einer Fläche. Es ist kein Objektname.

Im Folgenden werden die MultiSurf-Namen für Punkt-, Kurven- und Flächenarten verwendet. Das ergibt zwar „denglische“ Sätze, soll aber dem Verständnis und der Nachvollziehbarkeit dienen.

 

1 Rumpf

1.1 Knick durchlaufend – Segelboot

Wie sich ein Bootsrumpf mit Längsknick erzeugen läßt, ist in Tutorium 2 „Rundspantrumpf mit durchlaufendem Knick“ beschrieben (Modell sy15_full_length_chine.ms2). Der Rumpf besteht aus zwei Flächen mit gemeinsamer Längskante. Für die Seite wird der Flächentyp Developable Surface verwendet, der Boden ist analog wie bei einem Standard-Rundspanter eine C-spline Lofted Surface. Entlang der Längskante bilden die Flächen einen zum Bug hin in Spantrichtung schwächer werdenden Knick.

Modell sy15_full_length_chine.ms2 – die Seite des Rumpfes ist eine Developable Surface, der Boden ist eine C-spline Lofted Surface mit 6 Masterkurven und je 4 Kontrollpunkten (Tutorium 2).

 

1.2 Knick auslaufend – Segelboot

Die Modellierung eines Rumpfes mit auslaufendem Längsknick ist Thema von Tutorium 3 „Rundspantrumpf mit auslaufendem Knick“.

Modell sy15_vanish_chine2.ms2 – allmählich auslaufender Knick. Die hinteren Mcs für Seite und Boden stoßen in Spantrichtung mit einen Knick aneinander, die vorderen Mcs schließen tangential aneinander an (Tutorium 3).

Der Rumpf im Modell sy15_vanish_chine2.ms2 setzt sich ebenfalls aus einer Fläche für die Seite und einer Fläche für den Boden zusammen. Beide sind wie bei einem Standard-Rundspanter erzeugt. Damit der Längsknick allmählich ausläuft, stoßen die hinteren Mcs in Spantrichtung mit einen Knick aneinander, die vorderen Mcs schließen tangential aneinander an.

Modell sy15_vanish_chine2.ms2 – allmählich auslaufender Knick (Tutorium 3

 

1.3 Knick auslaufend – Jolle

Bei den beiden vorangehenden Formaufgaben wird die Rumpffläche durch zwei Teilflächen gebildet, die entlang der Knicklinie beziehungsweise ihrer Verlängerung aneinander anschließen. Im Modell dinghy.ms2 besteht der Rumpf aus einer einzigen C-spline Lofted Surface, deren Masterkurven von Oberkante Rumpf bis Bodenkontur durchlaufen.

Modell dinghy.ms2 – allmählich auslaufender Knick. Von Oberkante Rumpf bis Bodenkontur durchlaufende Masterkurven stützen eine einzige C-spline Lofted Surface.

Bis auf den Bugbereich sind die Masterkurven PolyCurves, deren Komponenten (B-spline Curves) mit Knick aneinander stoßen.

 

1.4 Knick auslaufend – Motorboot

Sollen bei einem Motorbootrumpf die Spanten im Vorschiffsbereich stark ausfallen, kann mit einem auslaufenden Knick verhindert werden, dass das Deck übermäßig breit wird. Modell powerboat_vanish_chine.ms2 ist eine Anwendung der vorstehend beschriebenen Methode, eine einzige Fläche mit Knick zu modellieren. Mc2 und Mc3 sind PolyCurves; ihre Komponenten jeweils eine Line und eine B-spline Curve, die mit einem Knick aneinander anschließen. Alle übrigen Mcs der C-spline Lofted Surface sind B-spline Curves.

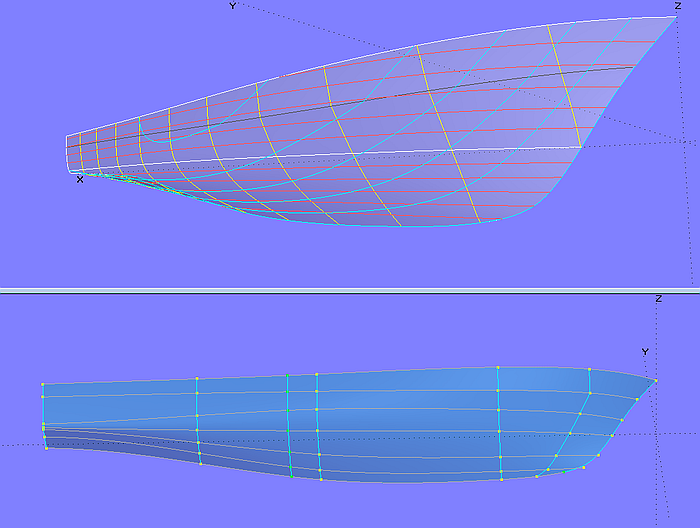
Modell powerboat_vanish_chine.ms2 – C-spline Lofted Surface mit auslaufendem Knick; Mc2 und Mc3 sind PolyCurves.

 

Modell powerboat_vanish_chine.ms2

 

1.5 Gerade Bodenschnitte

Im Tutorium 17 „B-spline-Kurven und B-spline-Flächen“ wird an Hand des Modells bottom.ms2 die Konstruktion einer speziell geformten Bodenfläche eines Motorbootrumpfes beschrieben. Die Entwurfsforderung lautet, dass ab einer bestimmten Längsposition die Schnitte exakt gerade verlaufen.

Dazu ist die Bodenfläche in ein Bugteil und ein Heckteil unterteilt. Die Basisfläche des geraden Heckteils ist eine Translation Surface, aufgespannt mit einer Line in Längsrichtung und einer B-spline Curve in Querrichtung, die die Spantform des Heckteils bestimmt. Den vorderen Teil der Bodenfläche bildet eine B-spline Lofted Surface, gestützt von 5 Mcs. Die vorderen 3 Mcs sind freie B-spline Curves, aber die beiden letzten Mcs liegen als B-spline Snakes auf der Heckfläche. Dadurch läuft die Bugfläche tangential in die Heckfläche ein.

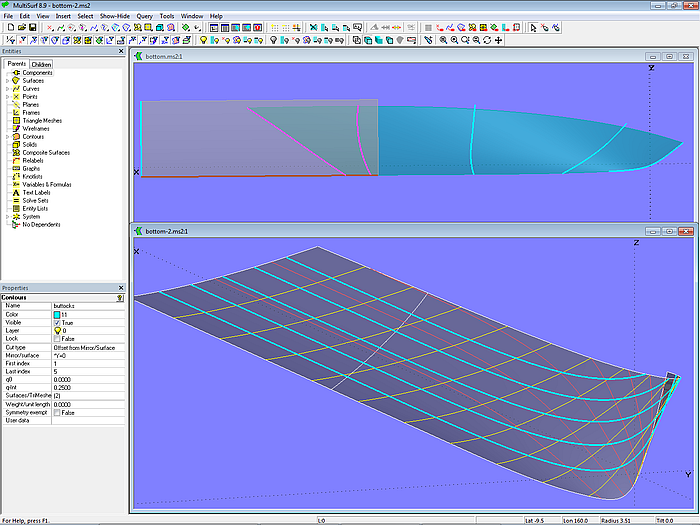
Modell bottom.ms2 – Bodenfläche mit exakt geradem Verlauf der Schnitte im Hinterschiff (Tutorium 17)

 

1.6 Boden mit Propellertunnel

Ebenfalls Im Tutorium 17 „B-spline-Kurven und B-spline-Flächen“ wird im Modell tunnel_stern.ms2 gezeigt, wie ein Propellertunnel in die Bodenfläche eines Motorbootrumpfes eingefügt werden kann. Basisfläche des Bodens ist eine C-spline Lofted Surface, die Tunnelfläche eine B-spline Lofted Surface mit 6 in Längsrichtung verlaufenden Mcs.

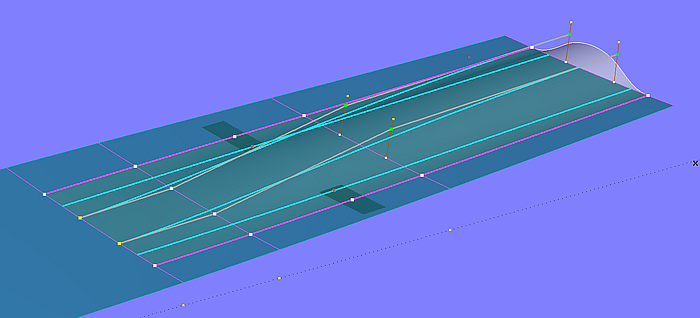
Modell tunnel_stern.ms2 – Propellertunnel als B-spline Lofted Surface mit 6 Mcs (Tutorium 17)

Die Rand-Mcs sind B-spline Snakes auf der Bodenfläche, die beiden mittleren Mcs B-spline Curves, die Größe und Verlauf der Tunnelhöhe in Quer- und Längsrichtung formen. Den tangentialen Einlauf des Tunnels in den Boden stellen zwei Procedural Curves sicher. Deren Konstruktion sorgt dafür, dass jeder ihrer Kurvenpunkte auf der Tangentialebene im korrespondierenden Kurvenpunkt auf der jeweils benachbarten Rand-Mc liegt.

Die fertigen Teilflächen des Bodens werden durch SubSurfaces erzeugt.

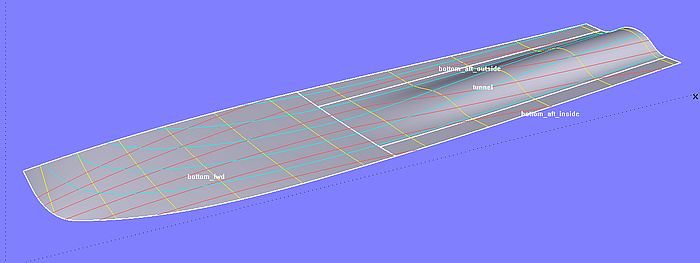
Modell tunnel_stern.ms2 – die fertigen Teilflächen des Bodens werden durch SubSurfaces erzeugt (Tutorium 17).

 

1.7 Spritzleiste

Modell sprayrail-1.ms2

Modell sprayrail-1.ms2 zeigt, wie sich mit wenig Aufwand eine Spritzleiste erzeugen läßt, die ab einem bestimmten Punkt mit konstanter Breite verlaufen soll.

Für die Konstruktion einer Spritzleiste läßt sich zweckmäßig eine Relative Curve verwenden. Die Eltern einer Relative Curve sind eine Basiskurve sowie zwei Punkte. In diese Punkte werden Anfangs- und Endpunkt der Basiskurve versetzt, alle dazwischenliegenden Punkte der Basiskurve werden interpoliert. Mit einem Graph kann man die Interpolation dieser Zwischenpunkte beeinflussen, um zum Beispiel den hinteren Punkt stärker zu gewichten als den vorderen.

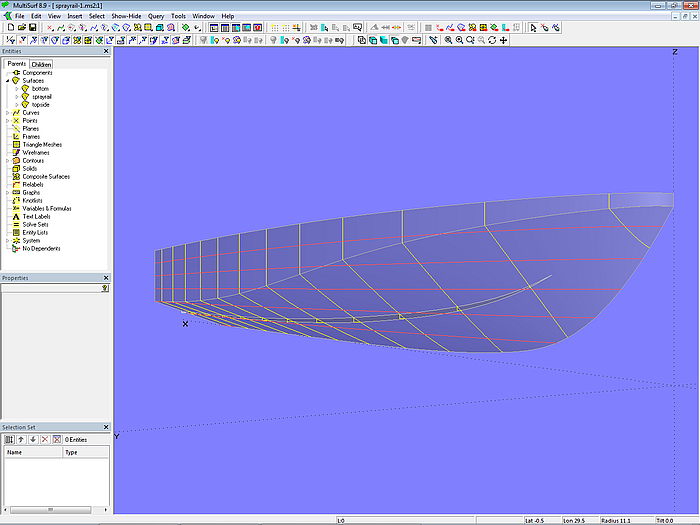
Modell sprayrail-1.ms2 – Konstruktion einer Spritzleiste mit Relative Curve

Ausgangspunkt für die Innenkante der Spritzleiste ist die B-spline Curve sp_c0. Sie liegt in der XY-Ebene und wird als Projected Snake sp_n0 auf den Boden des Rumpfes projeziert. Im Anfangspunkt (t = 0) von sp_n0 liegt der Ring ring1, im Endpunkt (t = 1) der Ring ring2. In Y-Richtung versetzt zu ring2 ist Point p1; er bestimmt die Breite der Spritzleiste.

Die Aussenkante der Bodenfläche der Spritzleiste wird durch die Relative Curve sp_c1 gebildet. Eltern sind als Curve die Snake sp_n0, als Point1 der Ring ring1, als Point2 der Point p1 sowie der B-spline Graph h1.

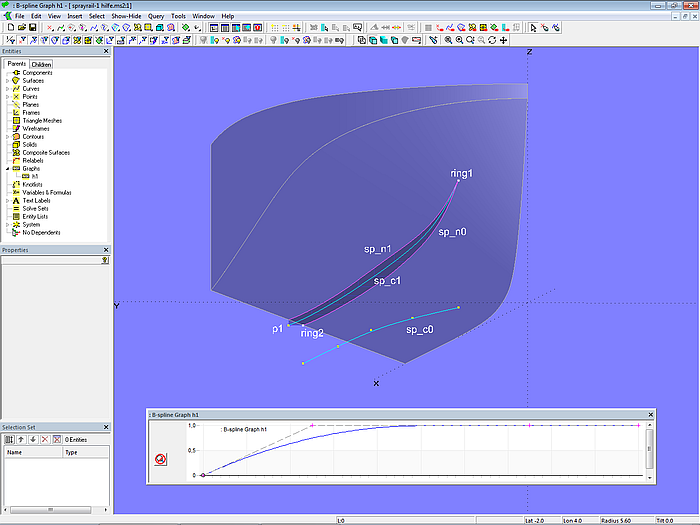
Modell sprayrail-1.ms2 – mit einem B-spline Graph kann der Verlauf einer Relative Curve modifiziert werden.

Der B-spline Graph h1 hat 4 Werte, der Anfangswert ist Null, die anderen Werte sind gleich 1. Dies bewirkt, daß nur am Anfang der Relative Curve der Punkt ring1 eine Rolle spielt, dann ab einer gewissen Distanz nur noch der Point p1. Der Verlauf des B-spline Graph läßt sich mit Hilfe der Funktion View/ Display/ Profile/ Graph anzeigen.

Für die Seite der Spritzleiste wird die Relative Curve sp_c1 senkrecht zur XY-Ebene auf den Boden projeziert (Projected Snake sp_n1). Mit den 3 Masterkurven sp_n1, sp_c1 und sp_n0 wird abschließend die B-spline Lofted Surface sprayrail erzeugt.

Der Vorteil dieser Konstruktion ist die Einfachheit. Aber man muß etwas mit der Anzahl der Werte gleich 1 für den B-spline Graph h1 experimentieren, um den Bereich mit konstanter Breite für die Spritzleiste festzulegen.

 

Modell sprayrail-2.ms2

Ganz analog zum Objekt PolyCurve gibt es das Objekt PolyGraph. Es setzt sich aus mehreren B-spline Graphen zusammen. Im Modell sprayrail-2.ms2 kontrolliert der B-spline Graph h1 die Zunahme der Spritzleiste von Null bis zur maximalen Breite. Der B-spline Graph h2 bewirkt, dass die Breite konstant bleibt. Der PolyGraph h3 bindet beide zusammen. Zunahme und konstante Breite muß so nicht mit einem einzigen Graph geregelt werden, was es übersichtlicher macht. Außerdem hat der PolyGraph noch den Vorteil, dass man über seine end t-values festlegen kann, über welche Distanz die einzelnen Graphen jeweils bestimmend sind. Im Beispielmodell übernimmt ab t = 0.25 der B-spline Graph h2, die Relative Curve ist also ab 25% der Basiskurve zu ihr parallel und damit die Breite der Spritzleiste konstant.

 

Modell sprayrail-3.ms2

Modell sprayrail-3.ms2 zeigt ein Beispiel, wie man eine Spritzkante modellieren kann, die mit einem etwas weniger spitzen Frontteil beginnt, nach einer gewissen Distanz eine maximale Breite erreicht, und die dann bis zum Heck konstant bleibt.

Ausgangspunkt für die Innenkante der Spritzleiste ist wiederum die B-spline Curve sp_c0 in der XY-Ebene. Sie wird als Projected Snake sp_n0 auf den Boden projeziert. In Anfangspunkt (t = 0) von sp_n0 liegt der Ring ring1, im Endpunkt (t = 1) der Ring ring3. Die Länge des Vorderteils der Spritzkante bestimmt Ring ring2, den anschließenden Hauptteil zwischen ring2 und ring3 definiert die SubSnake sp_n1. Diese ist die Basiskurve für die Relative Curve sp_c1. Die beiden Punkte p1 und p2 (relativ zu ring2 und ring3) legen mit ihren dy- und dz-Koordinatenwerten die Anfangs- und Endbreite sowie die seitliche Neigung des Hauptteils der Spritzleiste fest.

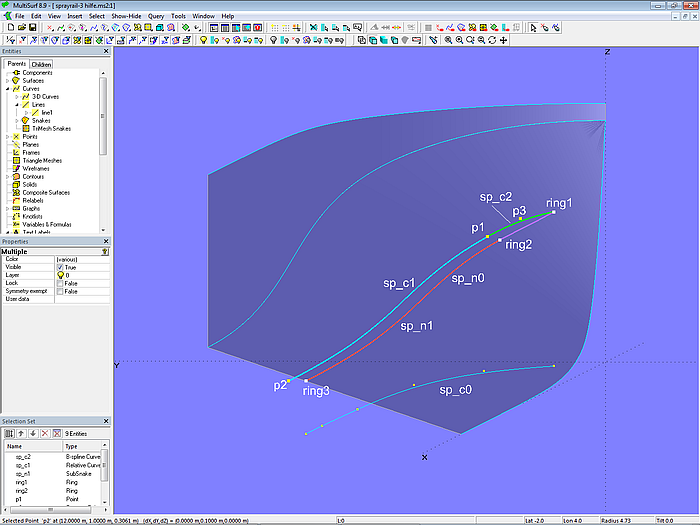
Modell sprayrail-3.ms2 – Spritzleiste mit völligem Frontteil

Die B-spline Curve sp_c2 kontrolliert die Zunahme der Breite im Vorderteil. Der Tangent Point p3 stellt sicher, dass sp_c2 ohne Knick an die Relative Curve sp_c1 anschließt. Beide Kurven werden als PolyCurve sp_c3 zusammengefaßt, die dann ihrerseits vertikal als Projected Snake sp_n2 auf den Boden projeziert wird.

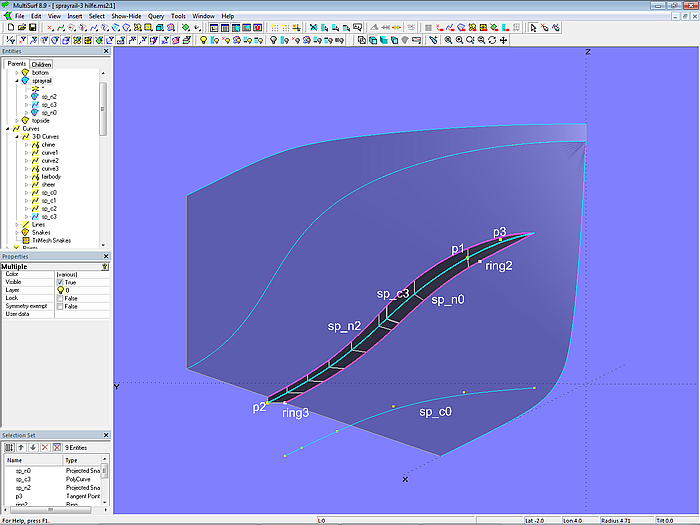
Modell sprayrail-3.ms2 – Spritzleiste mit völligem Frontteil

Mit den 3 Masterkurven sp_n0, sp_c3 und sp_n2 wird abschließend die B-spline Lofted Surface sprayrail erzeugt.

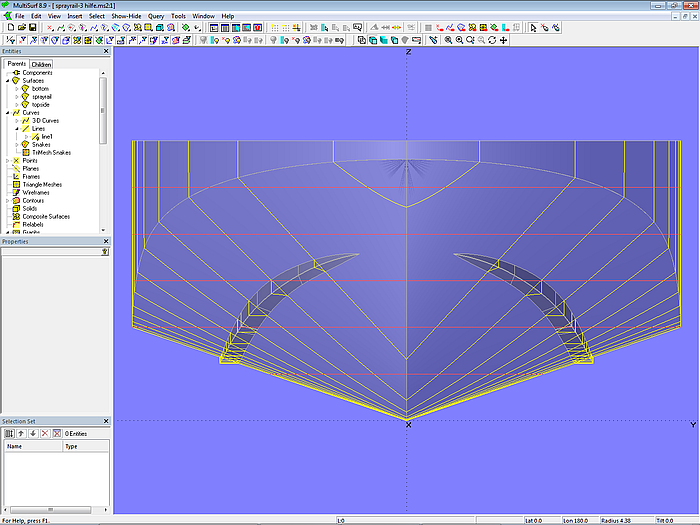
Modell sprayrail-3.ms2 – Spritzleiste mit völligem Frontteil

 

1.8 Auslaufende Spritzkante

Im Tutorium 12 „Auslaufende Spritzkante“ wird ausführlich über verschiedene Methoden berichtet, wie man eine Spritzkante modellieren kann, die sich nur über einen Teilbereich des Rumpfes erstreckt.

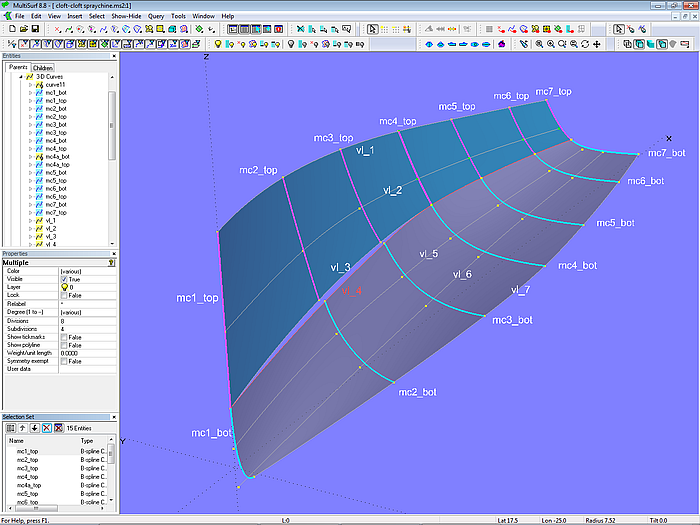
Modell cloft-cloft-spraychine.ms2 – Anordnung der Masterkurven und der Hilfskurven für den Strak der beiden C-spline Lofted Surfaces Seite und Boden (Tutorium 12)

 

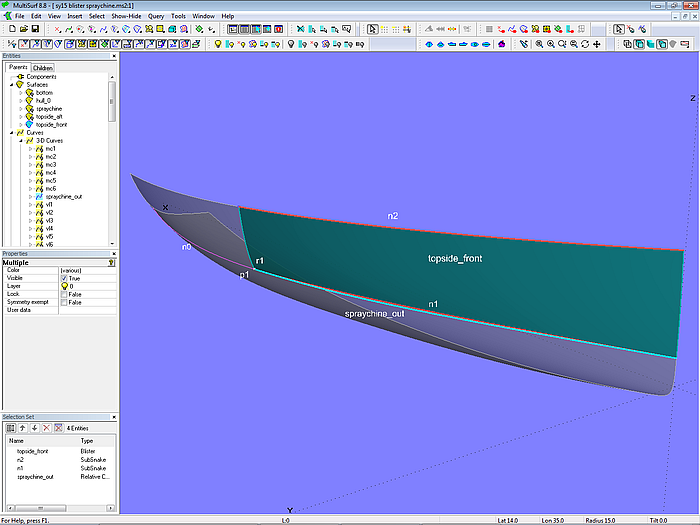
Modell blister-spraychine.ms2 – Blister-Fläche topside_front (Tutorium 12)

 

1.9 Fußreling

Modell washrail.ms2 demonstriert, wie sich bei einem Bootsrumpf aus Metall eine Fußreling modellieren läßt. Entwurfsforderung ist konstante Breite der Oberseite, die Innenseite soll senkrecht zum Deck stehen.

Ausgangspunkt ist die Rumpffläche hull_0 vom Typ C-spline Lofted Surface (5 Mcs mit je 5 Cps). Die Decksfläche deck_0 ist ebenfalls eine C-spline Lofted Surfaces mit gleicher Anzahl Masterkurven. Bei jeder Deck-Masterkurve liegt der erste Cp als XYZBead auf der korrespondierenden Rumpf-Mc, und zwar um die Höhe der Fußreling unter dem ersten Cp der Rumpf-Mc. Diese Anordnung hat den Vorteil, dass man beim Entwurf den fertigen Freibord sieht, das heißt, die Rumpfoberkante ist gleich der Oberkante der Fußreling, der Rumpf wird nicht um die Fußreling höher.

Das Maß, um das der erste Cp der Decks-Mcs unter Oberkante Rumpf liegt, wird durch die Variable washrail_height bestimmt. So kann man zum einen die Höhe der Fußreling rasch ändern. Zum anderen bleibt die Höhe gleich, wenn die Oberkante des Rumpfes geändert wird.

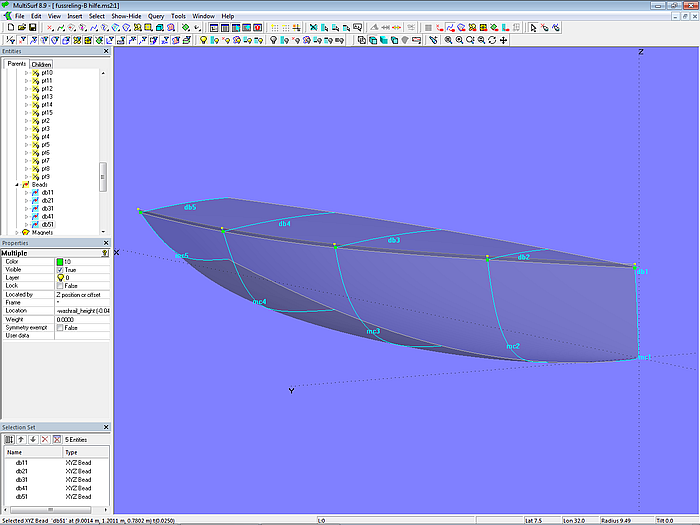
Modell washrail.ms2 – Aussenkante Deck liegt um die Höhe der Fußreling unter Oberkante Rumpf. Der erste Cp jeder Deck-Mc ist ein Bead auf der korrespondierenden Rumpf-Mc.

Zunächst wird entlang der Aussenkante der Basisfläche des Decks (C-spline Lofted Surface deck_0) die EdgeSnake oe_deck_0 erzeugt. Auf ihr liegt der Ring r1, von dem seinerseits der Tangent Point pt1 und der Offset Point pt2 abhängen. Die Line l0 verbindet r1 und pt2. Um diese Line wird pt1 um 90° gedreht (Rotated Point pt3), dieser dann auf das Deck projeziert als Projected Magnet m0.

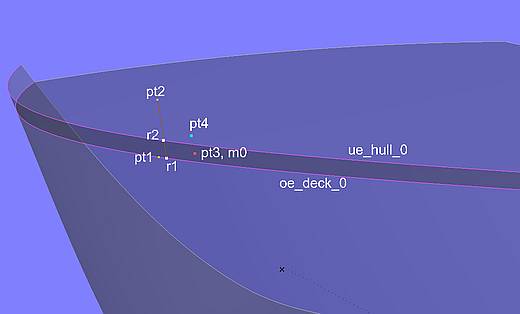
Modell washrail.ms2 – Definition eines Kurvenpunktes für die prozedurale Konstruktion der Innenkante der Fußreling

An der Position von Ring r1 wird dann die Oberkante des Rumpfes (EdgeSnake ue_hull_0) geschnitten im XYZRing r2. Mit den so erzeugten drei Punkten r1, m0 und r2 ist der Punkt pt4 definiert als Copy Point.

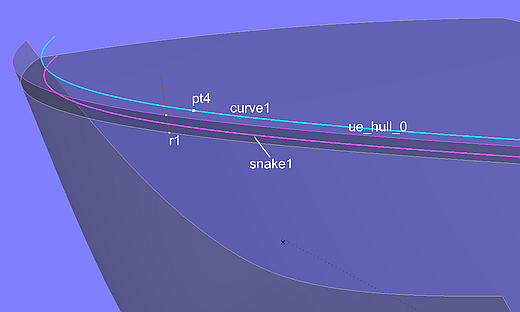
Modell washrail.ms2 – Konstruktion der Innenkante der Fußreling als Procedural Curve

Diese Konstruktion des Punktes pt4 wird nun für alle Positionen des Rings r1 wiederholt durch die Procedural Curve curve1. Snake1 ist deren Projektion senkrecht auf die Deckfläche.

Die Fußreling washrail wird erzeugt als B-spline Lofted Surface mit den drei längslaufenden Kurven ue_hull_0, curve1 und snake1.

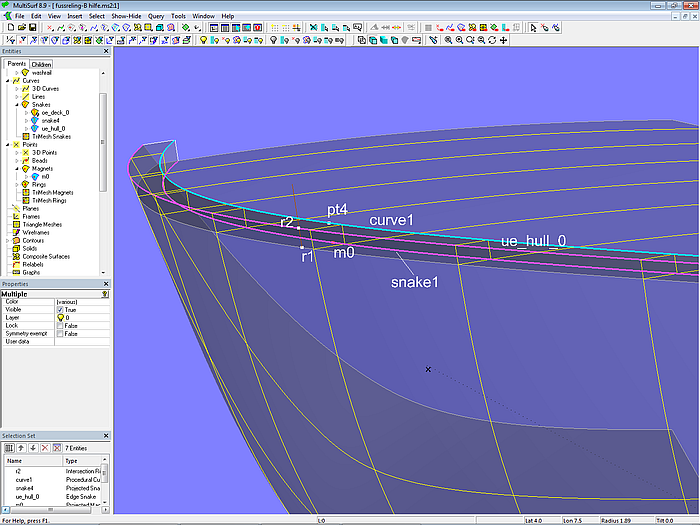
Modell washrail.ms2

 

2 Abrundungen

2.1 Bugrundung

Im Tutorium 8 “On the rounding of bows, sterns, sharp waterlines and on the attachment of keels” werden verschiedene Konstruktionen für Bugrundungen vorgestellt. Die vom Autor bevorzugte Methode soll nun an Hand des Modell tangent_bowround-2.ms2 gezeigt werden.

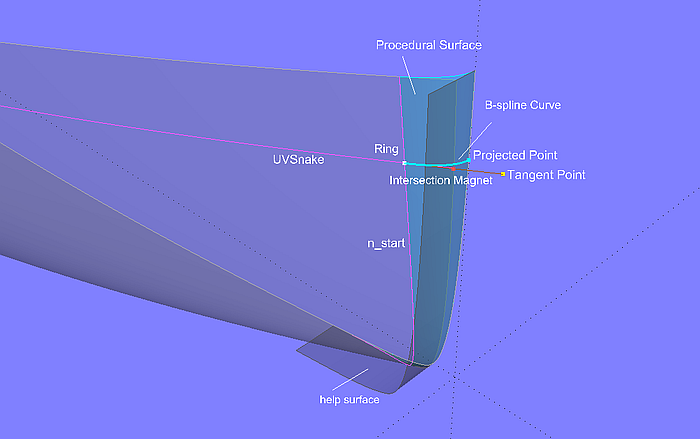
Modell tangent_bowround-2.ms2 – tangential anschließende Bugrundung mit einer Procedural Surface

Auf der Snake n_start, die den Beginn der Bugrundungsfläche bestimmt, befindet sich der Ring ring1 als Support einer in Längsrichtung verlaufenden UVSnake. Die Tangente an der Position von ring1 wird dann mit Hilfe des Tangent Points pt3 auf dieser Snake erzeugt. Die Line von ring1 nach pt3 schneidet die Vorstevenhilfsfläche (zur Mittschiffsebene senkrechtstehend) im Intersection Magnet m3. Dieser Intersection Magnet wird dann als Projected Point pt4 auf die Mittschiffsebene projiziert. Die Punkte ring1, m3 und pt4 sind jetzt die Eltern der B-spline Curve curve1. Schließlich wird die Konstruktion dieser Kurve durch eine Procedural Surface für alle Positionen von ring1 wiederholt. Das heißt, die sich bewegende Kurve der Procedural Surface ist curve1, der Antriebspunkt ist ring1.

Hinweis:
Es ist wichtig, dass die Tangente die Hilfsfläche schneidet (Intersection Magnet m3). Schneidet die Hilfsfläche die Tangente in einem Intersection Bead und verwendet man diesen als Eltern für pt4 und curve1, nimmt die Berechnung der Bugrundungsfläche mehr Zeit in Anspruch.

 

2.2 Deckrundung 1

Rolling Ball Fillet

Modell deck_round-1.ms2 demonstriert, wie die Kante zwischen Deck und Rumpf mit Hilfe von Flächen vom Typ Rolling Ball Fillet abgerundet werden kann.

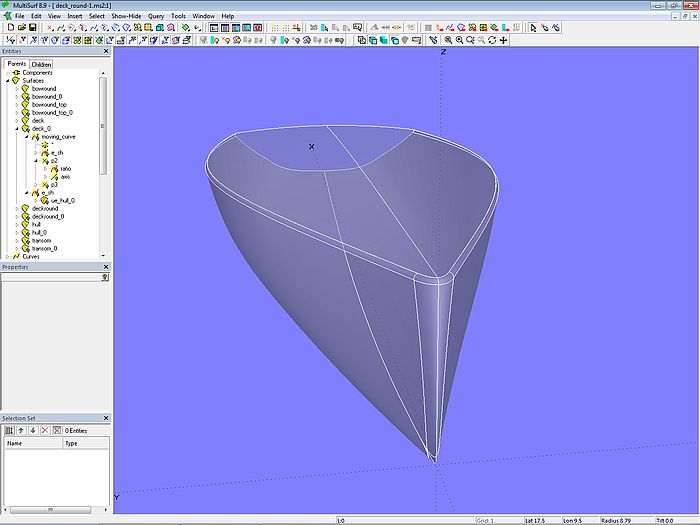
Modell deck_round-1.ms2 – Abrundung zwischen Rumpf und Deck mit Rolling Ball Fillets

Ausgangspunkt sind die Basisflächen hull_0 und deck_0, die entlang der Oberkante Rumpf aneinander anschließen, sowie die Abrundung des Vorstevens bowround_0. Die Rundung zwischen Rumpf und Deck erfolgt durch das Rolling Ball Fillet deckround_0, die Rundung zwischen Vorsteven und Deck durch das Rolling Ball Fillet bowround_top_0. Die Variable radius bestimmt die Größe beider Abrundungen.

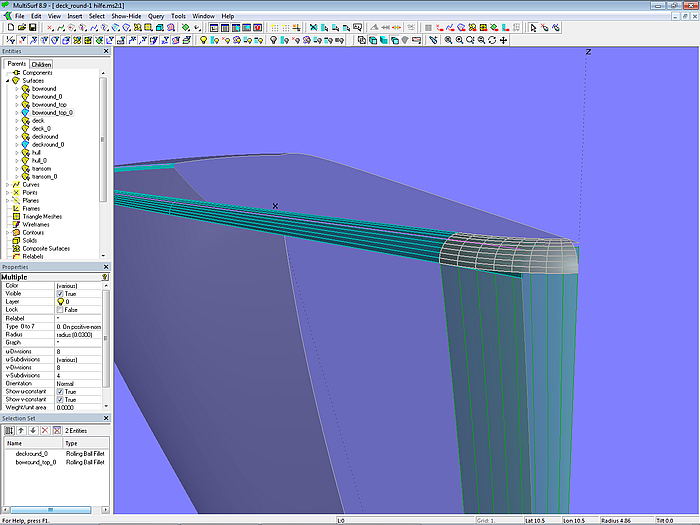
Modell deck_round-1.ms2 – Abrundung zwischen Rumpf und Deck mit Rolling Ball Fillets

Um die nicht überdeckten Flächenteile zu erhalten, werden Rumpf, Deck und Bugrundung abschließend an den Rundungsflächen abgeschnitten (SubSurface hull, Trimmed Surface deck, Trimmed Surface bowround).

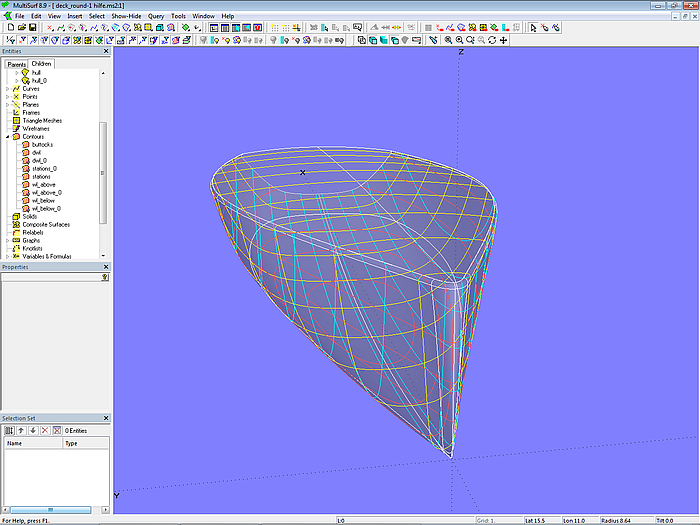
Modell deck_round-1.ms2 – Abrundung zwischen Rumpf und Deck mit Rolling Ball Fillets

 

2.3 Deckrundung 2

Während in Modell deck_round-1.ms2 die Abrundung zwischen Rumpf und Deck mit einem relativ kleinen Radius erfolgt, der über der Länge konstant ist, ist im Modell deck_round-2.ms2 die Rundung zwischen Rumpf und Deck eine Freiformfläche.

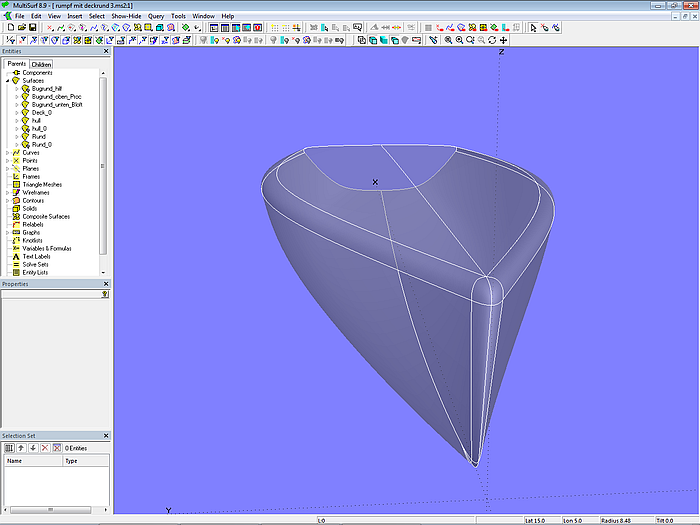
Modell deck_round-2.ms2 - große Deckrundung

Die Basisflächen von Rumpf und Deck (hull_0, deck) sind C-spline Lofted Surfaces mit je 5 B-spline-Masterkurven. Auch für die Basisfläche der Abrundung zwischen Rumpf und Deck (deckround_0) wird dieser Flächentyp verwendet.

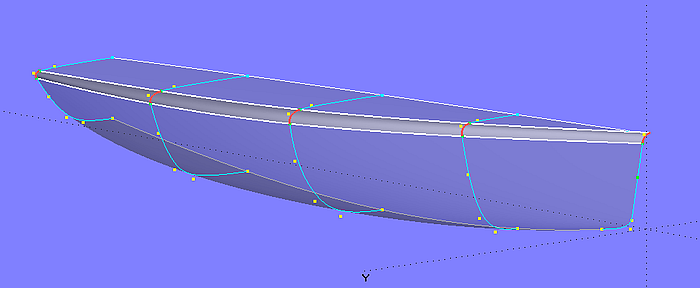
Modell deck_round-2.ms2 – Basisflächen von Rumpf, Deck und Abrundung als C-spline Lofted Surfaces

Die Mcs der Abrundung werden mit je 3 Kontrollpunkten bestimmt. Dabei ist Cp1 ein Bead auf der Verbindungslinie zwischen dem ersten Kontrollpunkt der Rumpf-Mc und dem 2. Kontrollpunkt der Decks-Mc. Und Cp3 ist ein Bead auf der Verbindungslinie zwischen dem ersten und dem 2. Kontrollpunkt der Rumpf-Mc. Auf diese Weise wird der tangentiale Anschluß der Abrundungs-Mc sowohl zur Rumpf- wie auch zur Decks-Mc hergestellt.

Als Beispiel sei Masterkurve 3 betrachtet. Die B-spline Curve mc3_round wird definiert mit dem Bead e31, dem Point p31 sowie dem Bead e32. e31 liegt auf der Line l_31, die Point p31 und p32 (Cp1 und Cp2 der Rumpf-Mc) verbindet. Der Bead e32 wiederum liegt auf der Line l_32 zwischen Point p31 und Point d32, dem Cp2 der Decks-Mc.

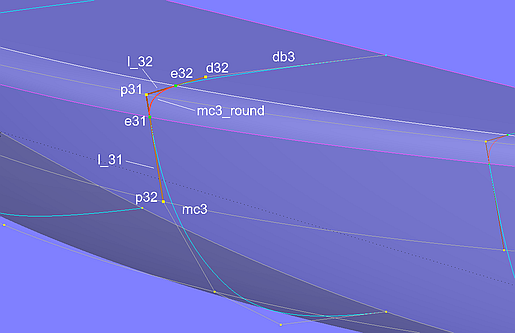
Modell deck_round-2.ms2 – tangentialer Anschluß der Abrundungs-Mc an die Mcs von Rumpf und Deck

Die Rundung des Rumpfes am Bug ist herkömmlich mit der B-spline Lofted Surface bowround ausgeführt. Kontrollkurven (Eltern) sind die Snake n0 auf dem Rumpf, die den Beginn der Abrundung bestimmt, die erste Kontrollkurve des Rumpfes mc1 und dessen Projektion auf die Mittschiffsebene, die Projected Curve c0.

Die Abrundung bowround_top, die den Übergang zwischen Bugrundung (bowround), Deck (deck) und Rumpf-Deck-Rundung (deckround_0) herstellt, ist eine Tangent Boundary Surface. Ihre Definition benötigt 4 Kurven. Curve1 ist die EdgeSnake le_deck entlang der Vorderkante des Decks (deck), curve2 ist die B-spline Curve c1 auf der Mittschiffsebene, die mit Hilfe von 2 Tangent Points tangential zu Mitte Deck sowie zu Mitte Bugrundung verläuft. Curve3 ist die EdgeSnake ue_bowround, die Oberkante der Bugrundungsfläche bowround, curve4 ist die B-spline Snake n2, die den Einlauf von bowround_top in die Rumpf-Deck-Rundung deckround_0 festlegt. Durch Vorgabe entsprechender Randbedingungen verläuft die Tangent Boundary Surface bowround_top tangential zur Bugrundung, zur Rumpf-Deck-Rundung und zum Deck sowie normal zur Mittschiffsebene.

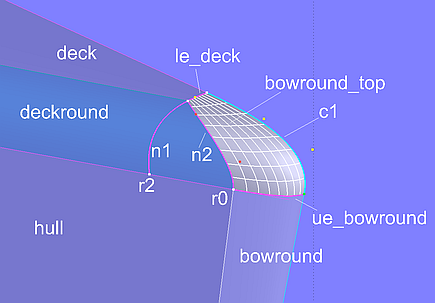
Modell deck_round-2.ms2 – die Tangent Boundary Surface bowround_top ist tangential zu den angrenzenden Flächen sowie normal zur Mittschiffsebene.

Modell deck_round-2.ms2

 

2.4 Abgerundete Aufbaukanten

Mit dem Flächentyp Rolling Ball Fillet lassen sich auch die Kanten entlang des Aufbaudachs abrunden. Tutorium 13 „Decks und Aufbauten“ zeigt Beispiele.

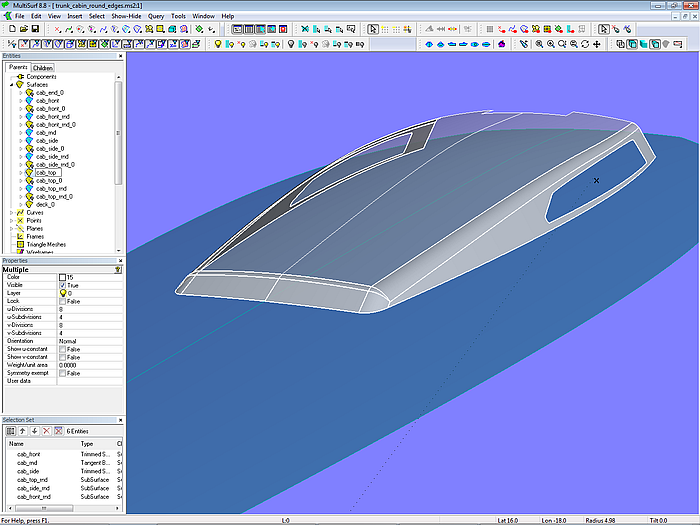
Modell trunk_cabin_round_edges.ms2 – Abrundung der Aufbaukanten mit Rolling Ball Fillets (Tutorium 13)

 

2.5 Abrundung Randbogen Kielflosse

Der Randbogen einer Kielflosse soll abgerundet werden. Modell fin_keel_tipround.ms2 zeigt, wie für diese Aufgabe eine Blend Surface eingesetzt werden kann. Mit einer Blend Surface kann eine glatte Übergangsfläche zwischen zwei Flächen erzeugt werden.

Die Basisfläche der Kielflosse ist die C-spline Lofted Surface fin_keel_0, die über 3 Masterkurven vom Typ Foil Curve aufgespannt wird.

Modell fin_keel_tipround.ms2 – Abrundung des Randbogens mit einer Blend Surface

Die gerade Kielsohle bottom_fin_keel ist eine Ruled Surface, aufgespannt zwischen der unteren Kiel-Mc mc_3 und der SubCurve c0. Deren beiden Beads e3 und e4 begrenzen dieses Teilstück der Profilsehne chord_3.

Eine Blend Surface benötigt 4 Supports, zwei Snakes auf Fläche 1 und zwei Snakes auf Fläche 2. Den Beginn der Blend Surface fin_keel_tipround bestimmt die Snake sn1. Im Beispiel ist dies eine einfache Line Snake zwischen je einem Ring auf der Kielhinterkante und Kielvorderkante. Entlang der Unterkante der Kielflosse verläuft die EdgeSnake sn2. Entlang der Aussenkante der Kielsohlenfläche bottom_fin_keel verläuft die EdgeSnake sn3, entlang ihrer Innenkante die EdgeSnake sn4. Damit sind für die Abrundung die erforderlichen Snakes auf den beiden Flächen bestimmt.

Mit den beiden Beads e3 und e4 kann die Abrundung in den Ecken verändert wrerden. Um nur den Umriß vorne abzurunden, verschiebt man e3 an das hintere Ende der Profilsehne chord_3.

Hinweis:
SubCurve c0 ist mit dem Relabel-Objekt label definiert.

Warum?

Die Geschwindigkeit einer Kurve ist die Änderungsrate der Entfernung (Bogenlänge) entlang der Kurve in Bezug auf die Änderung des t-Parameters. Beispielsweise ist ohne Relabel bei einer Line oder einem Arc die Geschwindigkeit konstant - gleiche t-Intervalle haben genau gleiche Bogenlängen. Bei einer B-spline Curve hängt die Geschwindigkeit jedoch vom Abstand zwischen den Kontrollpunkten ab. Sie ist in Regionen niedrig, in denen zwei oder mehr Kontrollpunkte nahe beieinander liegen, und relativ hoch, wenn die Kontrollpunkte weit voneinander entfernt sind. Bei den meisten Kurvenarten ist die Geschwindigkeit in Bezug auf t variabel.

Man kann die Geschwindigkeitsverteilung entlang einer Kurve visualisieren durch Anzeigen der Tickmarks (Properties Manager). Liegen die Tickmarks eng beieinander, ist die Geschwindigkeit gering, liegen sie weiter auseinander, ist sie hoch. Alternativ kann man die Kurvengeschwindigkeit auch über View/Display/Profile/Velocity Profile anzeigen.

Die Masterkurven der Kielflosse fin_keel_0 sind Foil Curves. Deren Geschwindigkeit in Bezug auf t ist an der Profilnase (t = 1) gleich Null. Dies wird an alle davon abhängigen Snakes vererbt. Darum haben drei der die Blend Surface definierenden Snakes (Line Snake sn1 und die EdgeSnakes sn2 und sn3) am Kurvenende (t = 1) ebenfalls eine Kurvengeschwindigkeit gleich Null. Damit die Blend Surface fin_keel_tipround harmonisch verläuft, muß dies auch bei der vierten Snake (sn4) der Fall sein. Diese ist EdgeSnake der Ruled Surface bottom_fin_keel_0, die zwischen der unteren Kiel-Mc mc_3 und der SubCurve c0 aufgespannt ist. Hat c0 am (t = 1)-Ende die Kurvengeschwindigkeit gleich Null, wird dies an sn4 als EdgeSnake weitervererbt.

Darum gehört zur Definition von c0 das Relabel-Objekt label mit den Werten {0, 1, 1}. Dieses Relabel sorgt dafür, dass am (t = 1)-Ende von c0 die Kurvengeschwindigkeit gleich Null ist.

Ohne Relabel für c0 verlaufen die Spanten im vorderen Bereich der Blend Surface fin_keel_tipround nicht rund, sondern spitz.

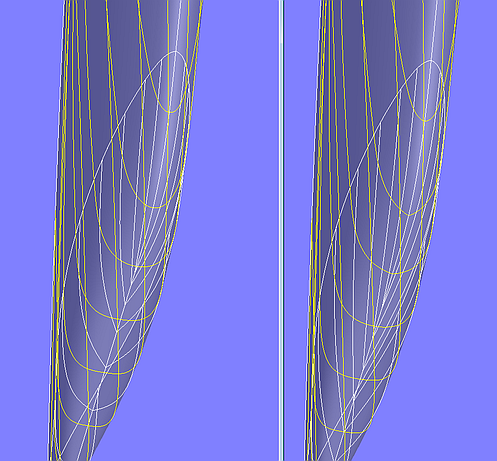
Modell fin_keel_tipround.ms2 – Einfluß der Kurvengeschwindigkeit der SubCurve c0 auf die Form der Blend Surface. Links: c0 mit Relabel. Rechts: c0 ohne Relabel

Modell fin_keel_tip.ms2 – Abrundung mit Blend Surface

 

2.6 Ausrundung Kielflosse - Ballast

In Tutorium 10 „Ballastkiele“ wird mit dem Modell bulb_revolution_surface.ms2 ein weiteres Beispiel gezeigt, wie sich mit einer Blend Surface auf einfache Weise ein Übergang zwischen Kielflosse und Ballastbulb gestalten läßt. Da die Konstruktion dort nicht weiter erklärt wird, sei es an dieser Stelle nachgeholt.

Basisfläche der Kielflosse ist die Ruled Surface keel_0, aufgespannt zwischen der Foil Curve root_keel_0 an der Kielwurzel und der Foil Curve tip_keel_0 an der Kielspitze. Der Ballastkörper ist die Revolution Surface bulb_0, deren Meridiankurve die Foil Curve bulb_meridian.

Für die ausrundende Blend Surface keel_fillet benötigen wir 4 Supports, zwei Snakes auf Fläche 1 und zwei Snakes auf Fläche 2. Die eine Snake auf Fläche 1 ist die B-spline Snake sn1; sie bestimmt den Beginn der Ausrundung auf der Kielflosse. Die andere Snake auf Fläche 1 ist die Intersection Snake sn2, in der keel_0 vom Ballast bulb_0 geschnitten wird. Diese Intersection Snake wird auf die Bulbfläche projeziert als Projected Snake sn3. Die andere Snake auf Fläche 2, also diejenige, die das Ende der Ausrundung auf der Bulbfläche festlegt, ist die B-spline Snake sn4, erzeugt mit 5 Kontrollmagneten. Mit diesen 4 Snakes ist die Blend Surface keel_fillet bestimmt.

Die nicht von der Ausrundung überdeckten Flächenbereiche der Kielflosse und des Ballstbulbs erzeugen die SubSurface keel und die SubSurface bulb.

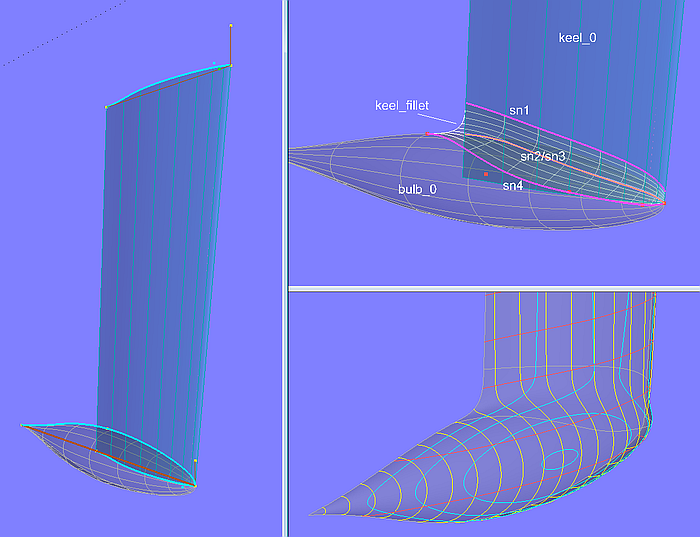
Modell bulb_revolution_surface.ms2 - Ausrundung mit Blend Surface zwischen Kielflosse und Ballastbulb (Tutorium 10)

Mit der Eigenschaft „Type“ der Blend Surface läßt sich der Verlauf der Ausrundung beeinflussen. Für Type = 1 ist der Randanschluß tangential, für Type = 2 sowohl tangential also auch krümmungstetig; die Ausrundung verläuft etwas enger.

So viel zum Thema Formmerkmale.

 

======================================================================================