Drei Konstruktionsaufgaben
Katamaran-Rumpf, Rumpf mit multi-konkavem Boden, Swath-Schiff: Übergang Auftriebskörper – Stützfläche
von Reinhard Siegel
Mai 2022
Inhalt
Einleitung
1 Katamaran-Rumpf
1.1 Formmerkmale
1.2 Aussenflächen Rumpf
Oberkante Seite
Bodenkontur
Vorderkante von Seite und Boden
Hinterkante von Seite und Boden
Innere Masterkurven
Flächen
1.3 Innenflächen Rumpf
Boden
Seite
2 Multi-konkaver Rumpf
2.1 Formmerkmale
2.2 Rumpf mit Standard-Boden
Oberkante Seite, Knick, Bodenkontur
Vorsteven – Vorderkante von Seite und Boden
Hinterkante von Seite und Boden
Innere Masterkurven
Rumpfflächen
2.3 Rumpf mit multi-konkavem Boden
Masterkurven – regelbasierter Ansatz
Masterkurven – Freiform-Ansatz
3 Swath-Schiff: Übergang Auftriebskörper – Stützfläche
3.1 Formmerkmale
3.2 Basismodell
3.3 Ausrundungsfläche 1 – Rolling Ball Fillet
3.4 Ausrundungsfläche 2 – Blend Surface
3.5 Anwendungsfall – Swath-Schiff
Modell-Aufbau
Rumpfflächen
Auftriebskörper und Stützfläche
Übergang Auftriebskörper–Stützfläche
Einleitung
Dieses Tutorium, angeregt durch einen MultiSurf-User, behandelt das Modellieren eines Katamaran-Rumpfes, eines multi-konkaven Bodens für ein Motorboot sowie des Übergangs zwischen zwei Flächen. Es geht darum, wie sich ganz bestimmte charakteristische Formmerkmale erzeugen lassen. Es geht nicht darum, Modelle mit spezifischen Abmessungen zu erstellen.
Verwendete Abkürzungen:
Cp: Kontrollpunkt, Stützpunkt (control point, support point); synonym verwendet
Mc: Masterkurve, Stützkurve (master curve, support curve); synonym verwendet
cp1, cp2, ...: bezeichnet den 1., 2. ... Punkt in der Liste der Kontrollpunkte einer Kurve. Es ist kein Objektname.
mc1, mc2, ...: bezeichnet die 1., 2. ... Kurve in der Liste der Stützkurven einer Fläche. Es ist kein Objektname.
Im Folgenden werden die MultiSurf-Namen für Punkt-, Kurven- und Flächenarten verwendet. Das ergibt zwar „denglische“ Sätze, soll aber dem Verständnis und der Nachvollziehbarkeit dienen.
1 Katamaran-Rumpf
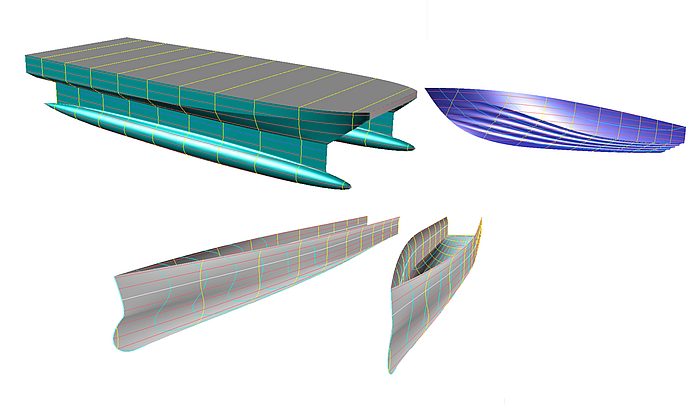
Ausgangspunkt ist ein Forschungsbericht über den Einfluß der Rumpfform auf die hydrodynamischen Eigenschaften von Hochgeschwindigkeits-Katamaranfähren. Das Geometriemodell einer der untersuchten Rumpfformen (S8) wird erstellt. Es ist kein Nachentwurf im Sinne von genauer Übereinstimmung, sondern es geht darum, die charakteristischen Formmerkmale zu modellieren. Am Beispiel des Modells s8-z.ms2 wird dies versucht.
Wenn im Weiteren von „Rumpf“ die Rede ist, ist nicht der Rumpf des gesamten Schiffes gemeint, sondern der eintauchende Schwimmkörper einer Schiffshälfte (Semi Hull).
1.1 Formmerkmale
Welche geometrischen Merkmale hat die Form von S8?
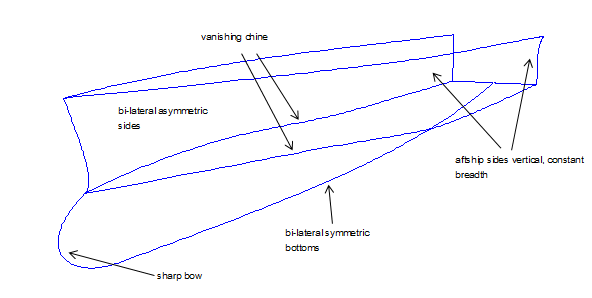
• Es gibt einen in Längsrichtung verlaufenden Knick, er läuft zum Bug hin aus. Dieser Knick trennt die
Rumpfflächen in Seite und Boden.
• Im hinteren Bereich sind die Seiten vertikal und konstant breit.
• Aussen- und Innenfläche des Bodens sind symmetrisch zu Mitte Rumpf.
• Aussen- und Innenfläche der Seite sind nicht symmetrisch zu Mitte Rumpf
• Wulstbug mit scharfen Wasserlinien
Wesentliches Formmerkmal ist der auslaufende Knick in der Rumpffläche. Tutorium 3 befaßt sich mit diesem Thema und beschreibt das prinzipielle Vorgehen, um eine solche Geometrie zu erzeugen.
Im vorliegenden Fall kommt hinzu, dass der Knick im hinteren Rumpfbereich in der Aufsicht gerade und mit konstanter Breite verläuft.
Für die Rumpf-Seiten sind wegen der Unsymmetrie zwei Flächen zu erzeugen. Die Aussenfläche des Bodens kann wegen der Symmetrie an der Rumpf-Mittelebene gespiegelt werden.
Anmerkungen zum Modell
Modell-Einstellungen (Tools/ Options/...)
.../ Model Units: Meters / Kilograms
.../ Performance: Decimal places = 4; Divisions multiplier = 2
.../ Dragging: Nudge amount = 0.01 [m]
Koordinatensystem
Statt des globalen Koordinatensystems wird als Koordinatensystem des Modells der 3-point Frame frame1 verwendet. Dadurch kann der gesamte Rumpf einfach an die gewünschte Breitenposition verschoben werden.
Mittelebene Rumpf
Die Mittelebene des Rumpfes ist die 2-point Plane plane1.
Verkürzte Darstellung
Wegen der besonderen Schlankheit des Rumpfes sind Ungenauigkeiten im Strak nicht leicht zu erkennen. Im Entwurfsstadium wird das Modell in X-Richtung um den Faktor 0.5 skaliert, ausgenommen die Cps der Bug-Masterkurven.
1.2 Aussenflächen Rumpf
Betrachten wir zunächst die Aussenflächen des Rumpfes (Semi Hull).
Es werden zwei in Längsrichtung verlaufende Flächen erzeugt, die C-spline Lofted Surface side_out für die Seite und die C-spline Lofted Surface bottom_out für den Boden. Seite und Boden sind entlang ihrer gemeinsamen Längskante verbunden. Sie stoßen im hinteren Rumpfbereich mit einem Knick aneinander, im vorderen Bereich sind sie in Spantrichtung tangential verbunden. Beide Flächen werden gestützt von B-spline-Masterkurven.
(Siehe auch die Tutorien 1 und 2; dort werden die Vorteile einer C-spline Lofted Surface mit B-spline Masterkurven und die Vertexkurven-Methode beschrieben.)
Beginnen wir mit dem Umriß beider Flächen, also Oberkante, Hinterkante, Unterkante, Vorderkante.
Oberkante Seite
Y-view: Verlauf von Bug bis Heck ist horizontal. Dies ist eine Annahme. Die Seite wird nach oben sicher weitergehen, die Mcs sind entsprechend nach oben zu verlängern.
Z-view: konstante Breite in der hinteren Hälfte.
Da eine C-spline Lofted Surface verwendet wird, muß durch Anzahl und Position der Cps dafür gesorgt werden, dass die Kurve nicht schwingt.
Es werden 9 Cps verwendet, alle definiert im 3-point Frame frame1. Durch diese Punkte der Oberkante Seite verläuft die C-spline Curve vl_1 (Vertexkurve, Strakhilfskurve). Die Eigenschaft „Dragging“ der Cps ist gesetzt auf Y-Richtung.
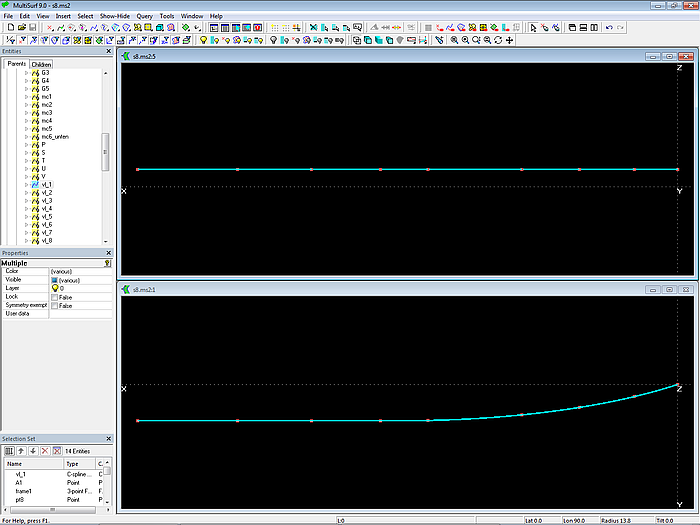
Modell s8-z.ms2 – Vertexkurve vl_1 beschreibt die Oberkante der Seite.
Über View/ Display/ Profile/ Curvature (oder den entsprechenden Toolbar Button) kann kontrolliert werden, dass die Kurve in eine Gerade einläuft.
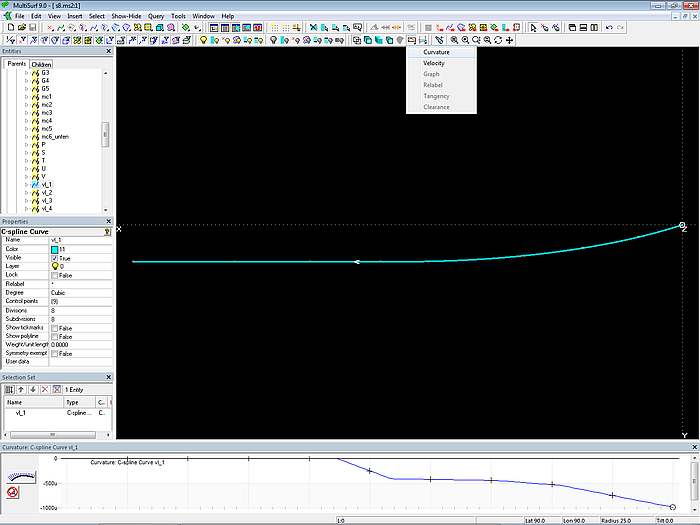
Modell s8-z.ms2 – Vertexkurve vl_1: Kontrolle des Krümmungsverlaufs über Profile/ Curvature
Bodenkontur
Analog wird die Strakhilfskurve (Vertexkurve) vl_7 für den Verlauf der Bodenkontur erzeugt. Für alle Cps ist dy = 0. Eigenschaft „Dragging“ gesetzt auf Z-Richtung.
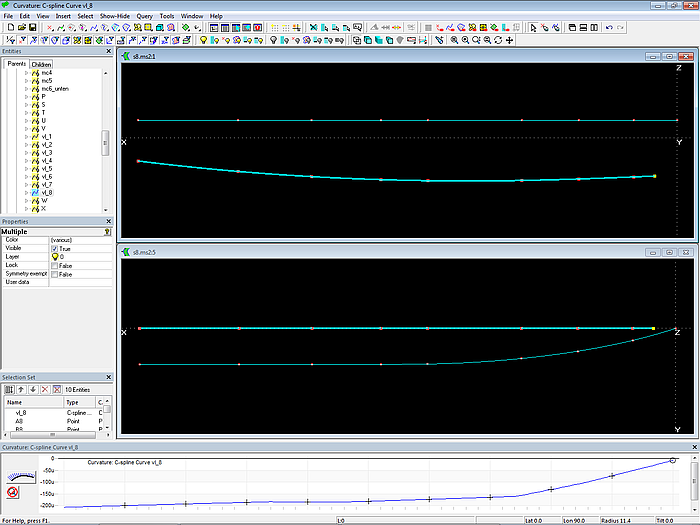
Modell s8-z.ms2 – Bodenkontur (Vertexkurve vl_7)
Vorderkante von Seite und Boden
B-spline Curve mc1_side und B-spline Curve mc1_bot - beide verlaufen in der Mittschiffsebene des Rumpfes. Also alle Cps definiert im 3-point Frame frame1 mit dy = 0. Eigenschaft „Dragging“ gesetzt auf X- und Z-Richtung.
Die Anzahl Cps (hier für beide Flächen 4) ist kein Dogma. Man verwende so viel, wie es nötig ist, um die gewünschte Form zu erzeugen. Eigenschaft „Degree“ der B-spline Curves gleich 3. Endpunkt von mc1_side (Bead e11) ist gleich Startpunkt von mc1_bot.
Beide Kurven sind tangential verbunden.
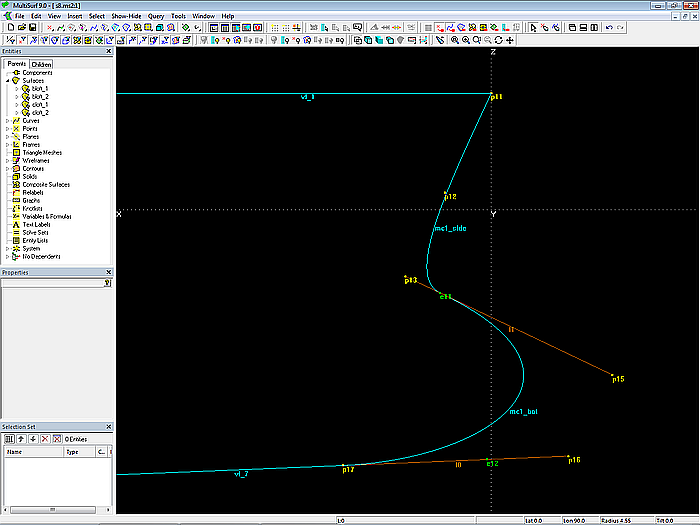
Modell s8-z.ms2 – Konstruktion der Mcs mc1_side und mc1_bot. Die tangentiale Verbindung ist festverdrahtet. Ebenso der tangentiale Einlauf in die Bodenkontur.
Man beachte auch, dass der vorletzte Cp (Bead e12) von mc1_bot auf der Tangente (Line l0) im Startpunkt der Vertexkurve vl_7 liegt. Damit ist der tangentiale Einlauf von mc1_bot in die Bodenkontur festverdrahtet.
Hinterkante von Seite und Boden
Seite vertikal: B-spline Curve mc9_side; für innere Cps: „Dragging“ = Z-Richtung.
Boden horizontal: B-spline Curve mc9_bot; für innere Cps: „Dragging“ = Y-Richtung
Beide Mcs verlaufen in Spantebene; für alle Cps: dx = 20 (Längen im Entwurfsstadium um Faktor 0.5 verkürzt).
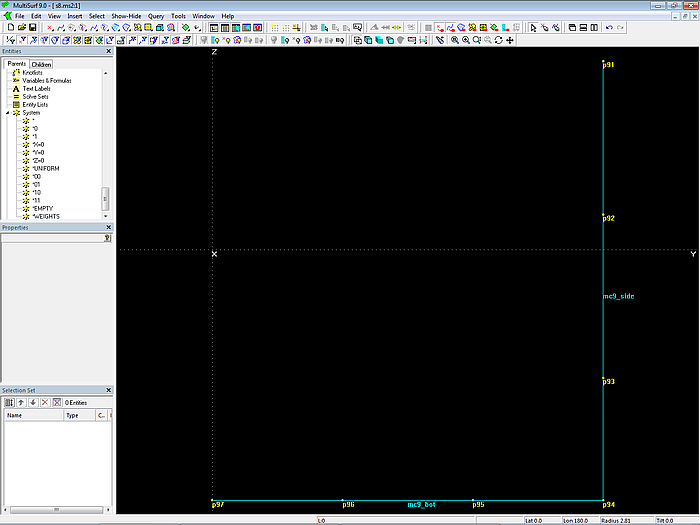
Modell s8-z.ms2 – Masterkurven am Heck: B-spline Curves mc9_side und mc9_bot
Damit sind Oberkante der Seitenfläche (vl_1), Unterkante der Bodenfläche (vl_7), sowie Vorder- und Hinterkante (mc1_side, mc1_bot, mc9_side, mc9_bot) des Rumpfes bestimmt.
Von der gemeinsamen Längskante von Seite und Boden sind bislang nur Beginn und Ende festgelegt, nämlich Bead e11 (Bug) und Point p94 (Heck).
Innere Masterkurven
Es müssen nun Mcs für das Innere beider Flächen erzeugt werden – 7 B-spline-Mcs für die Seite und 7 B-spline-Mcs für den Boden. Die Position dieser inneren Mcs sowie Start- und Endpunkt ist durch die Cps von vl_1 und vl_7 gegeben. Die Anzahl der Cps pro Mc ist 4, Degree = 3. Es kann somit mit der Vertexkurven-Methode gearbeitet werden, um strakende Flächen zu erzeugen.
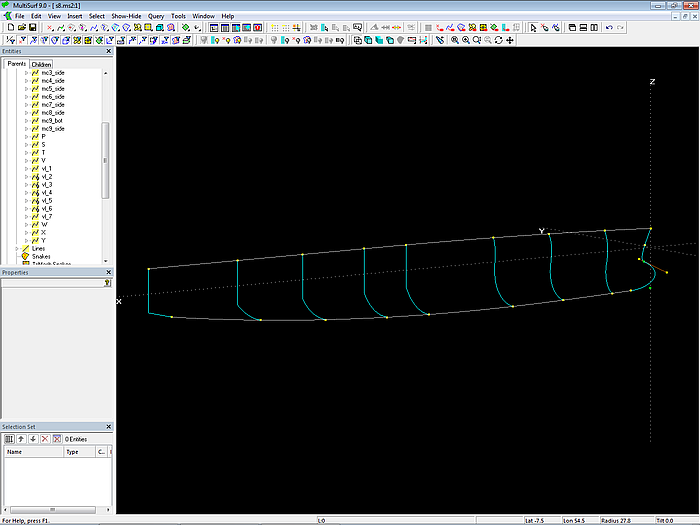
Modell s8-z.ms2 – Masterkurven der Außenflächen des Rumpfes
Die Mcs mc6_side bis mc8_side verlaufen vertikal. „Dragging“ der Cps gesetzt auf Z-Richtung.
Alle inneren Mcs verlaufen in Spantebene; folglich ist bei C-spline Lofted Surfaces die Form der Mc gleich der Form des Spantes am Ort der Mc.
„Dragging“ der Cps gesetzt auf Y und Z. Ein Cp kann dann in Perspektiv-Ansicht verschoben werden (dy, dz), ohne dass sich dx ändert.
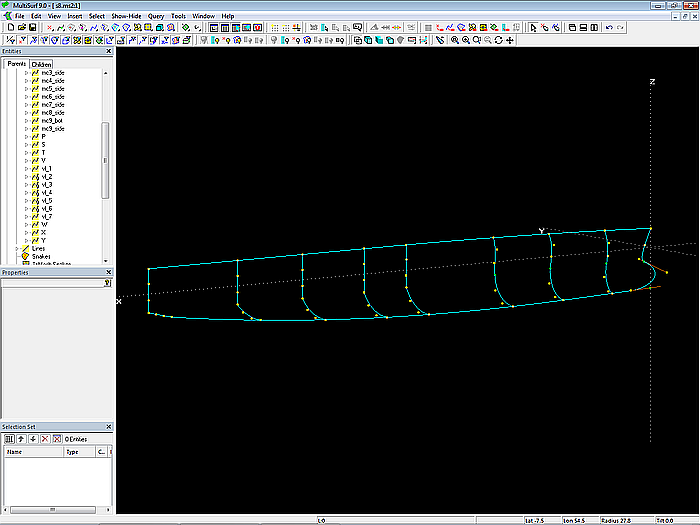
Modell s8-z.ms2 – Masterkurven und Kontrollpunkte für Seite und Boden der Rumpfaussenflächen
Zur Positionierung der Cps werden die C-spline Curves vl_2 bis vl_6 (Strakhilfskurven) durch die entsprechenden Cps der Mcs gelegt. Die gemeinsame Kante der Seiten- und der Bodenfläche beschreibt vl_4.
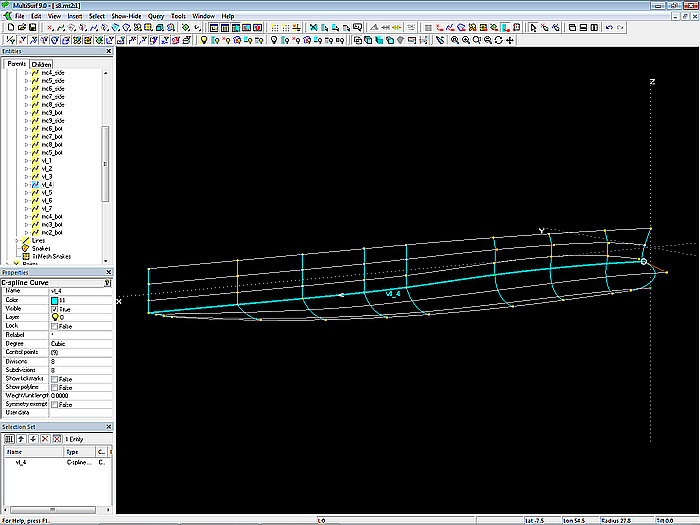
Modell s8-z.ms2 – Strakhilfskurven (Vertexkurven) zur Positionierung der Cps. Den Knickverlauf definiert vl_4.
Der tangentiale Anschluß der Mcs 2,3 und 4 erfolgt über die gleiche Konstruktion wie für die Mcs von Seite und Boden am Bug.
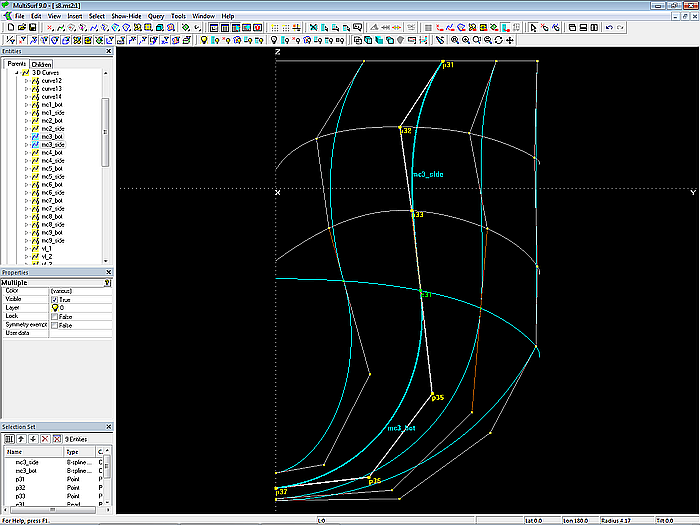
Modell s8-z.ms2 – tangentiale Verbindung der Mcs 2, 3 und 4
Flächen
Nach Definition der inneren Mcs können nun die beiden C-spline Lofted Surface side_out und bottom_out erzeugt werden. Anschließend werden durch diese die Contours Spanten, Schnitte und Wasserlinien gelegt.
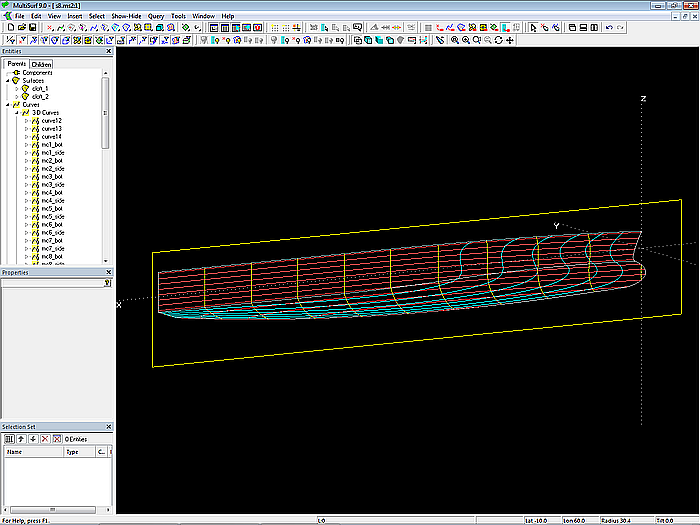
Modell s8-z.ms2 – Aussenflächen des Rumpfes (Länge verkürzt)
Soweit zur Konstruktion des Modells für die Aussenflächen des Katamaranrumpfes.
1.3 Innenflächen Rumpf
Boden
Bei der vorliegenden Geometrie sind für den Boden Aussen- und Innenfläche symmetrisch zur Mittelebene des Rumpfes. Die Boden-Innenfläche kann somit durch die Mirrored Surface bottom_in erzeugt werden.
Seite
Aussen- und Innenfläche der Seite sind nicht symmetrisch zur Mittelebene. Darum wird für die Seite die C-spline Lofted Surface side_in erzeugt: Ihre Mcs sind B-spline Curves mit je 4 Cps. Cp3 und Cp4 sind Mirrored Points der Cps der korrespondierenden Mcs für die Aussenfläche der Seite.
Änderungen der Aussenflächen side_out und bottom_out werden somit automatisch auf die Innenflächen side_in und bottom_in übertragen.
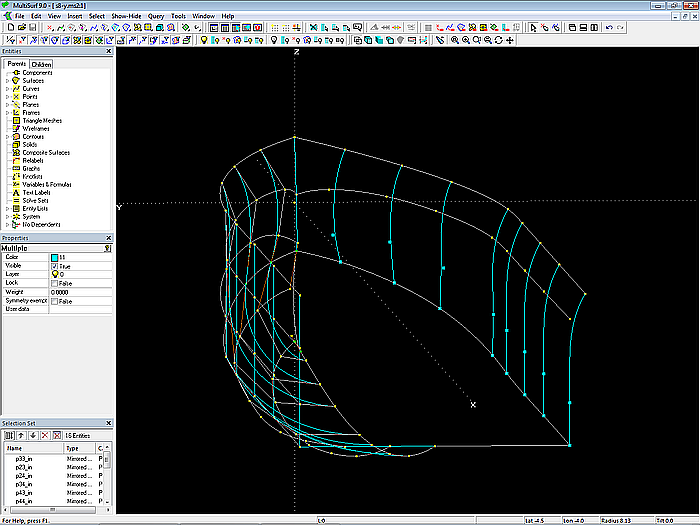
Modell s8-z.ms2 – Mcs für die Innenfläche der Seite – Cp3 und Cp4 sind Mirrored Points der Cps der korrespondierenden Mcs für die Aussenfläche der Seite.
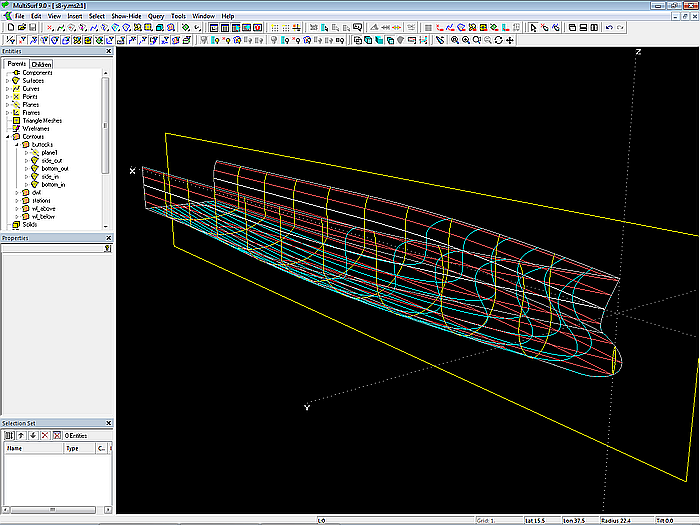
Modell s8-z.ms2 – Aussen- und Innenflächen des Rumpfes (Länge verkürzt)
Hinweis
Wie oben erwähnt, ist das Modell für das Entwurfsstadium in der Länge verkürzt. Um das Modell auf die wahre Länge zu bringen, müssen die X-Koordinaten der Cps mit dem Faktor 2 skaliert werden (Edit/ Transform/ Scale). Allerdings mit Ausnahme der Cps der Bug-Mcs. Um die Auswahl der zu skalierenden Punkte zu vereinfachen, gibt es die Entity List entities_to_scale. Diese im Entities Manager auswählen, dann Select/ Expand Entity List/ First Generation. Auf diese Weise kann zwischen Modell-Ansicht verkürzter und wahrer Länge gewechselt werden.
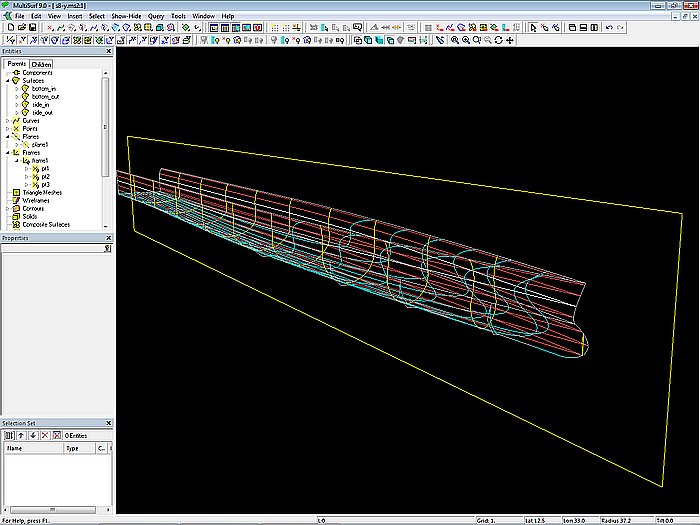
Modell s8-z.ms2 – Aussen- und Innenflächen des Rumpfes (wahre Länge)
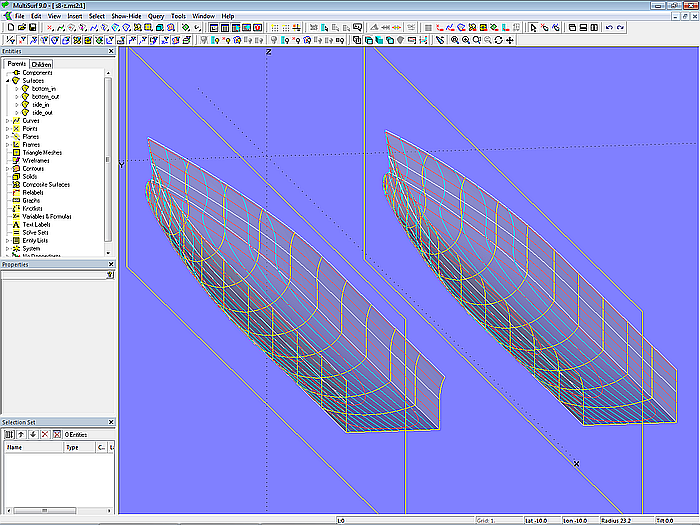
Modell s8-z.ms2 – Katamaran-Rumpf (wahre Länge)
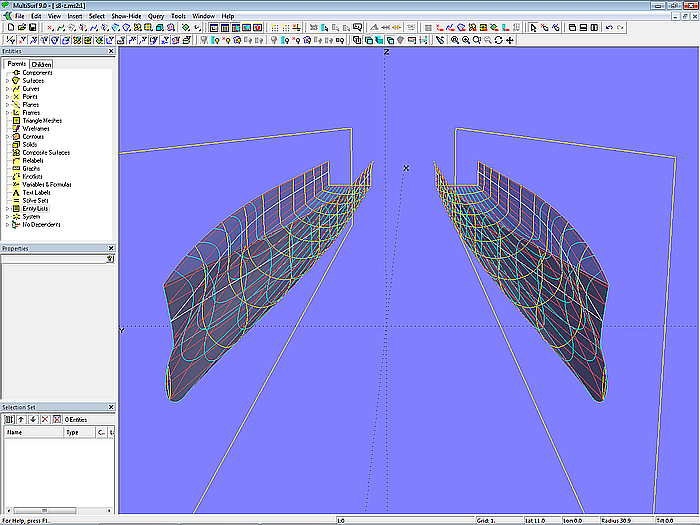
Modell s8-z.ms2 – Katamaran-Rumpf (wahre Länge)
2 Rumpf mit multi-konkavem Boden
Ausgangspunkt sind Bilder der Bodenfläche eines GFK-Motorbootes in seiner Laminierform sowie eine Ansicht des Spiegels. Der Boden hat Knicke in Längsrichtung, dazwischen ist er nach innen eingebuchtet.
Zunächst wird ein typischer Knickspant-Motorbootrumpf modelliert. Anschließend wird die Bodenfläche als Basis für eine Bodenfläche mit Einbuchtungen verwendet.
2.1 Formmerkmale
Schnelle Motorboote weisen auf die Bodenfläche aufgesetzte Spritzleisten auf. Zwischen diesen verläuft die Spantkontur normal. Im vorliegenden Fall zeigt die Bodenfläche mehrere in Längsrichtung verlaufende Knicke, zwischen diesen Knicken ist die Bodenfläche nach innen eingebuchtet (konkav). Die Spantform dieser Einbuchtungen oder Einkehlungen erinnert an eine Mischung von Spritzleiste und Tunnel.

Anmerkungen zum Modell
Modell-Einstellungen (Tools/ Options/...)
.../ Model Units: Meters / Kilograms
.../ Performance: Decimal places = 4; Divisions multiplier = 2
.../ Dragging: Nudge amount = 0.001 [m]
Koordinatensystem
Es wird das globale Koordinatensystems verwendet.
Mittelebene Rumpf
Die Mittelebene des Rumpfes ist die XZ-Ebene des globalen Koordinatensystems.
2.2 Rumpf mit Standard-Boden
Es wird ein typischer Knickspantrumpf für ein Motorboot angenommen. Er besteht aus zwei in Längsrichtung verlaufenden Flächen, die C-spline Lofted Surface side_0 für die Seite und die C-spline Lofted Surface bottom_0 für die Basisfläche Boden. Seite und Boden stoßen entlang ihrer gemeinsamen Längskante mit einem Knick aneinander. Beide Flächen werden gestützt von B-spline-Masterkurven.
Die Konstruktion von Knickspantrümpfen für Motorboote wird in Tutorium 4 ausführlich behandelt.
Zunächst werden die Umriße beider Flächen erzeugt, also Oberkante Seite, Knick, Bodenkontur sowie Vorsteven und Hinterkante von Seite und Boden.
Oberkante Seite, Knick, Bodenkontur
Den Verlauf von Oberkante Seite, Knick und Bodenkontur beschreiben die C-spline Curves vl_1, vl_3 und vl_5 (Vertexkurve, Strakhilfskurve). Sie werden jeweils mit 6 Cps definiert.
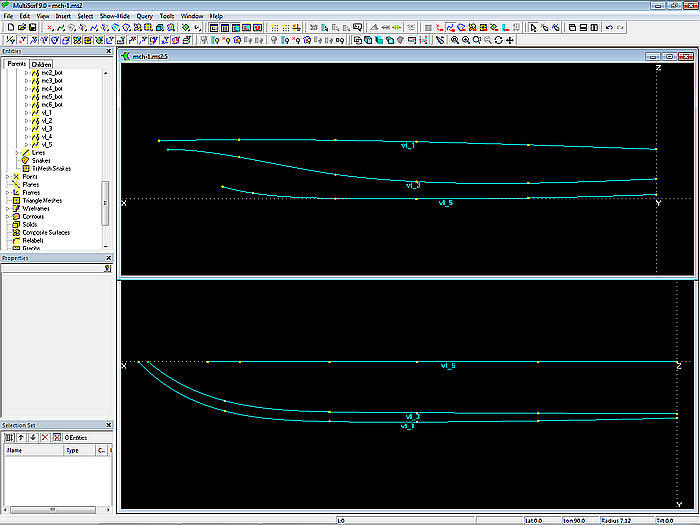
Modell mch-1.ms2 – Vertexkurven vl_1, vl_3 und vl_5 beschreiben den Verlauf von Oberkante Seite, Knick und Bodenkontur.
Über View/ Display/ Profile/ Curvature (oder den entsprechenden Toolbar Button) kann kontrolliert werden, ob der Krümmungsverlauf dieser Kurven harmonisch ist.
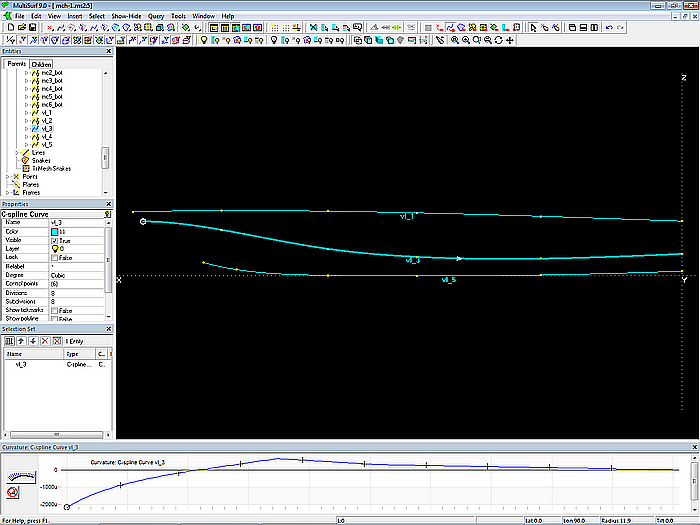
Modell mch-1.ms2 – Kontrolle des Krümmungsverlaufs der Vertexkurve vl_3 über Profile/ Curvature
Für alle Cps der Bodenkontur (vl_5) ist dy = 0. Die Eigenschaft „Dragging“ ist gesetzt auf Z-Richtung.
Vorsteven – Vorderkante von Seite und Boden
Den Verlauf des Vorstevens beschreiben die beiden mit je 3 Cps bestimmten B-spline Curves mc1_side und mc1_bot. Eigenschaft „Degree“ gleich 2.
Der vorletzte Cp (Bead e14) von mc1_bot liegt auf der Tangente (Line l0) im Anfangspunkt der Bodenkontur (vl_5). Durch diese Konstruktion läuft die Vorderkante der Bodenfläche tangential in die Bodenkontur ein.
Fest tangential verbunden sind auch die beiden Kurven mc1_side und mc1_bot. Dazu wird zuerst Line l1 aufgespannt zwischen Point p11 (Vorsteven-Kopf) und Bead e14 auf l0. Auf l1 liegt dann Bead e13 als Endpunkt von mc1_side und Startpunkt von mc1_bot.
Da der innere Cp von mc1_side ebenfalls auf Line l1 liegt, verläuft diese B-spline Curve gerade.
Freie Punkte sind nur Point p11 und Point p15, definiert mit dy = 0. Eigenschaft „Dragging“ gesetzt auf X- und Z-Richtung.
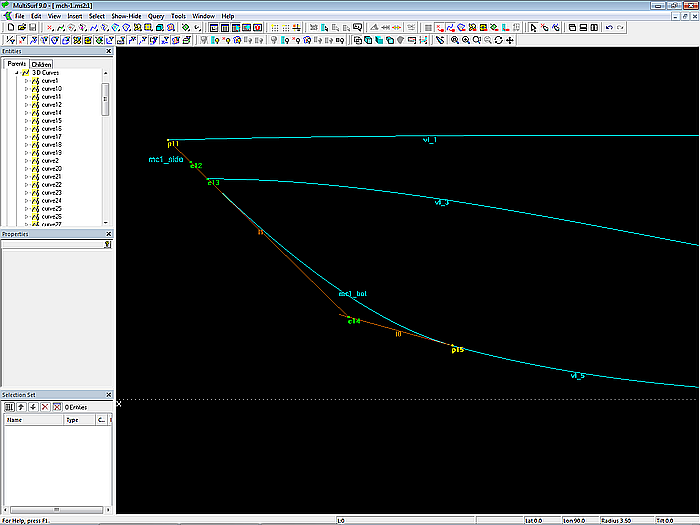
Modell mch-1.ms2 – Konstruktion der Mcs mc1_side und mc1_bot. Die tangentiale Verbindung ist festverdrahtet, ebenso der tangentiale Einlauf in die Bodenkontur.
Hinterkante von Seite und Boden
Sie werden gebildet durch die B-spline Curves mc6_side und mc6_bot. Beide Mcs verlaufen in Spantebene.
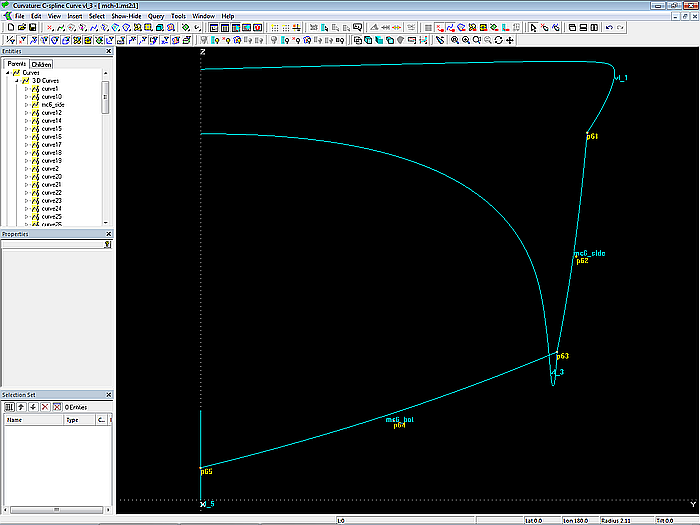
Modell mch-1.ms2 – Masterkurven am Heck: B-spline Curves mc6_side und mc6_bot
Damit sind Oberkante der Seitenfläche (vl_1), Unterkante der Bodenfläche (vl_5), Knick (vl_3) sowie Vorder- und Hinterkante (mc1_side, mc1_bot, mc6_side, mc6_bot) des Rumpfes bestimmt.
Innere Masterkurven
Es müssen nun die Mcs für das Innere beider Flächen erzeugt werden – 4 B-spline-Mcs für die Seite und 4 B-spline-Mcs für den Boden. Die Anzahl der Cps pro Mc ist 3, Degree = 2. Die Position der inneren Mcs sowie ihr Start- und Endpunkt ist durch die Cps von vl_1, vl_3 und vl_5 gegeben. Lediglich ein weiterer Cp muß jeweils dazwischen erzeugt werden.
Da alle Mcs vom gleichen Kurventyp mit jeweils gleicher Anzahl Cps sind, kann mit der Vertexkurven-Methode gearbeitet werden, um strakende.Flächen zu erzeugen. Entsprechend werden noch die beiden C-spline Curves vl_2 und vl_4 definiert.
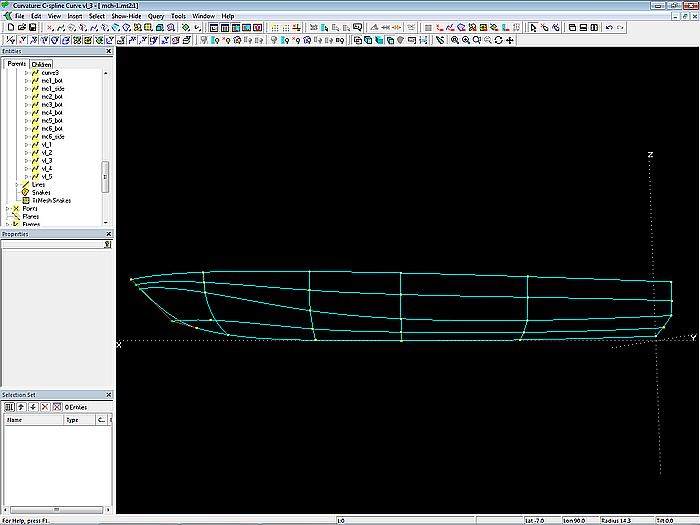
Modell mch-1.ms2 – Masterkurven, Kontrollpunkte und Vertexkurven der Rumpfflächen
Bis auf Vorsteven und mc2_bot verlaufen alle Mcs in Spantebene. „Dragging“ ihrer Cps gesetzt auf Y- und Z-Richtung. Sie können dann in Perspektiv-Ansicht verschoben werden (dy, dz), ohne dass sich dx ändert.
Rumpfflächen
Nach Definition der inneren Mcs können nun die beiden C-spline Lofted Surface side_0 und bottom_0 erzeugt werden. Anschließend werden durch diese die Contours Spanten, Schnitte und Wasserlinien gelegt.
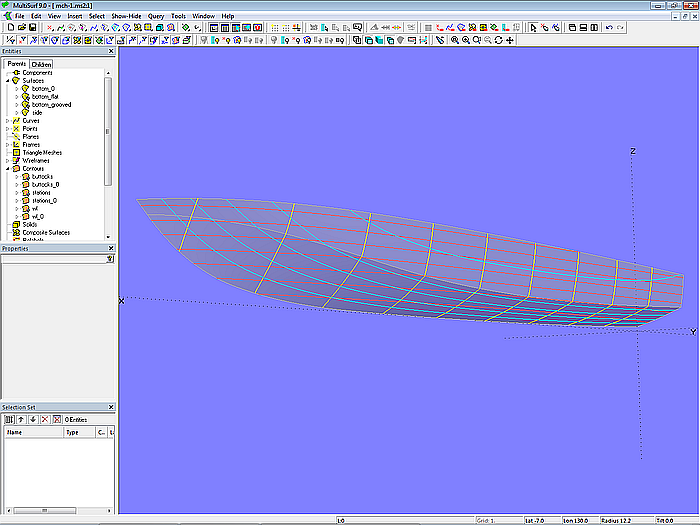
Modell mch-1.ms2 – Basisflächen Rumpf
Soweit zur Konstruktion des Modells für die Basisflächen des Motorbootrumpfes.
2.3 Rumpf mit multi-konkavem Boden
Masterkurven – regelbasierter Ansatz
Bei der vorliegenden Geometrieaufgabe soll der Boden nicht glatt sein, sondern in Längsrichtung verlaufende Einbuchtungen, Furchen, Einkehlungen aufweisen. Lediglich ein Flächenstreifen entlang der Bodenkontur ist Teil des bisherigen Bodens.
Auf Basis der vorhandenen Boden-Mcs werden neue Mcs mit Einkehlungen erzeugt. Mit diesen Mcs wird der multi-konkave Boden als C-spline Lofted Surface erzeugt.Dabei wird deren Form nicht frei definiert, also durch Kurven, deren Verlauf mit frei verschieblichen Punkte bestimmt wird. Vielmehr werden mit Hilfe von Variablen und Formeln sowie bestimmten Regeln geometrisch ähnliche Kurvenstücke erzeugt und dann mit einer PolyCurve zu einem Kurvenzug zusammengefaßt.
Es werden folgende Annahmen gemacht:
• Anzahl der Einkehlungen: 4
• Kurvenstück: B-spline Curve, 5 Cps, Degree = 2
- Anfangs- und Endpunkt liegt auf Mc für die Basisfläche Boden
- Gleiche Bogenlänge zwischen Anfangs- und Endpunkt an einer Mc
- Verlauf Kurvenanfang: gerade, horizontale Tangente
- Verlauf Kurvenende: vertikale Tangente
Die Trennkurve zwischen multi-konkavem Boden und glattem Boden wird durch die C-spline Curve vl_groove_4 definiert. Sie verläuft durch die Beads e14, e24, e34, e44, e54 und e64 auf den Mcs 1 bis 6 der Basis-Bodenfläche bottom_0.
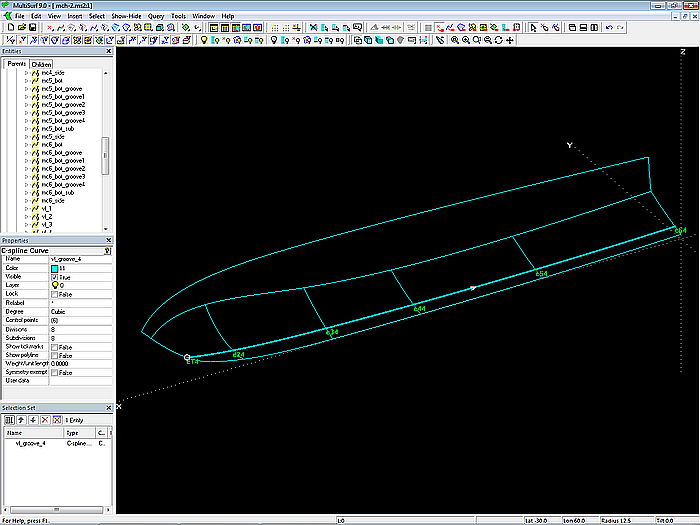
Modell mch-1.ms2 – Trennkurve zwischen multi-konkavem und glattem Boden
Am Beispiel von Mc5 soll die Konstruktion der neuen Mcs mit Einbuchtungen beschrieben werden.
Zunächst wird auf mc5_bot die Bogenlänge vom Kurvenanfang (t = 0) bis zum Bead e54 ermittelt und durch die Anzahl der Einkehlungen geteilt. Die Berechnung dieses Wertes erfolgt mit der Formel l_mc5_bot_groove. Mit dieser Bogenlänge als Abstand voneinander werden nun die drei Arc-length Beads e51, e52 und e53 auf mc5_bot erzeugt.
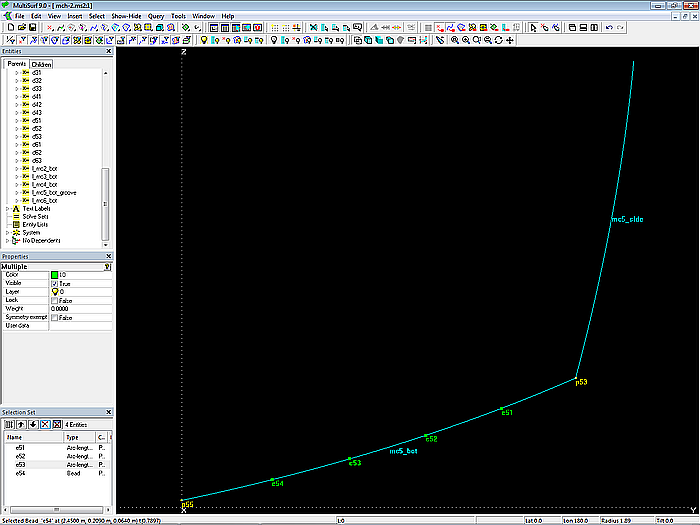
Modell mch-1.ms2 – Masterkurve mc5_bot mit 4 Beads im gleichen Abstand
Verschiebt man e54, ändert sich automatisch die Position der anderen Beads; die geometrische Beziehung (Teilung in 4 gleiche Bogenstücke) bleibt erhalten.
Mit Point p53 als Bezugspunkt wird nun Point g5_11 bestimmt, dx = 0,und dz = 0. Den Abstand dy bestimmt die Formel d51:
d51 = c2 * l_mc5_bot_groove
Die Variable c2 ist auf den Wert -0.145 gesetzt. Das heißt, Point g5_11 ist 14,5% der Einbuchtungsbreite nach innen versetzt relativ zu Point p53.
In analoger Weise wird Point g5_12 definiert. Den horizontalen Abstand von p53 bestimmt die Formel d52:
d52 = c3 * l_mc5_bot_groove
Die Variable c3 ist auf den Wert -0.65 gesetzt. Point g5_12 ist also 65% der Einbuchtungsbreite nach innen versetzt relativ zu Point p53.
In ähnlicher Weise wird Point g5_13 erzeugt, nun mit der Formel d53:
d53 = c4 * l_mc5_bot_groove
Die Variable c4 ist auf den Wert 0.21 gesetzt. Bezugspunkt von Point g5_13 ist e51, und er ist nicht horizontal versetzt, sondern vertikal – dz = d53.
Mit p52, g5_11, g5_12, g5_13 und e51 wird nun die B-spline Curve mc5_bot_groove1 bestimmt (Degree = 2).
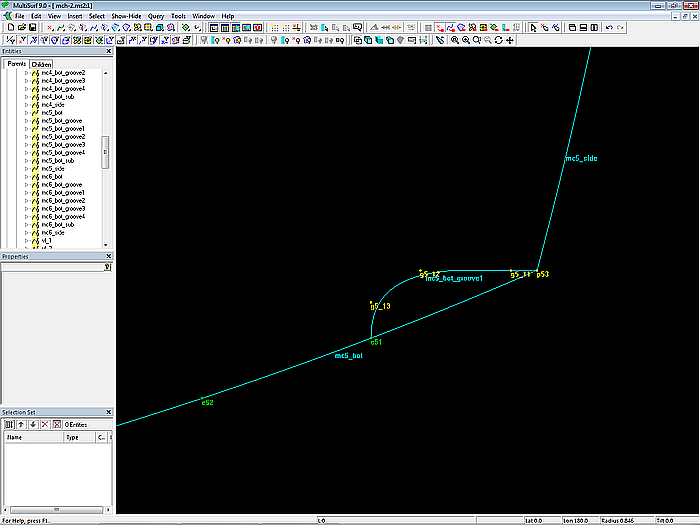
Modell mch-1.ms2 – Querschnitt von Einkehlung 1 an Mc5
Wie die Unterseite einer Spritzleiste verläuft mc5_bot_groove1 bis zur Mitte zwischen g5_11 und g5_12 gerade und horizontal.
Auf analoge Weise werden die übrigen Einkehlungen an Mc5 erzeugt.
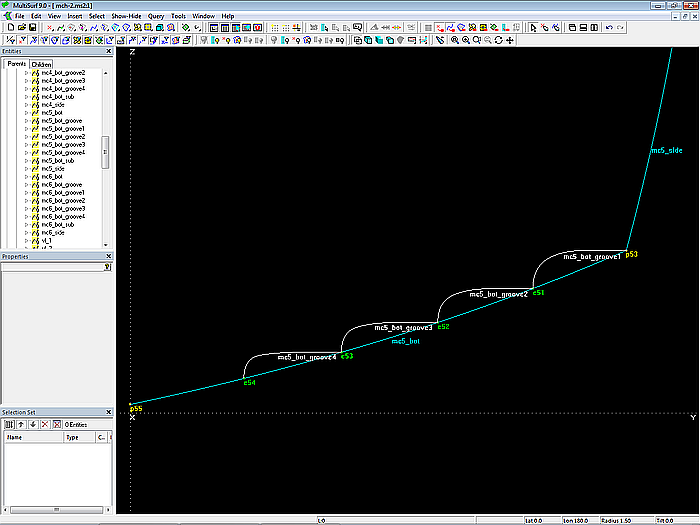
Modell mch-1.ms2 – B-spline Curves beschreiben den Querschnitt der Einkehlungen
Alle 4 Querschnitte werden nun zur PolyCurve mc5_bot_groove zusammengefaßt.
Die beschriebene Konstruktion wird dann für die Mcs 3, 4 und 6 wiederholt.
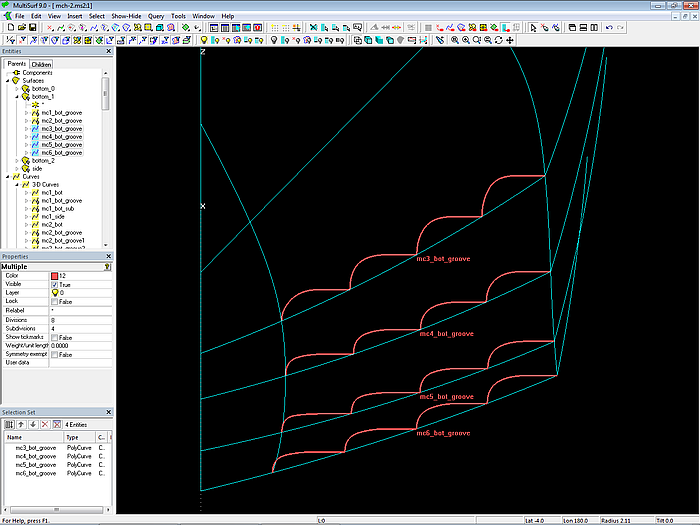
Modell mch-1.ms2 – Mcs (PolyCurves) für die multi-konkaven Bodenfläche
Etwas anders sehen die Einbuchtungen bei Mc2 aus. Hier wird als Querschnittsform ein Kreisbogen verwendet, der durch 3 Punkte verläuft. Auf den Mittelpunkt der Sehne des Kreisbogens bezieht sich die Buchthöhe. Sie ist definiert durch die Formel d2:
d2 = c1 * l_mc2_bot
Die Variable c1 ist auf den Wert 0.2 gesetzt.
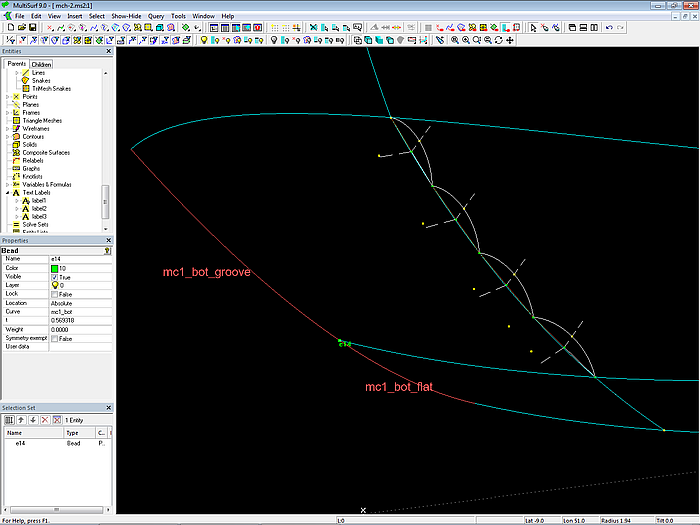
Modell mch-1.ms2 – an Mc2 sind die Querschnitte der Einbuchtungen Kreisbögen.
Fehlt noch die Bug-Mc des multi-konkaven Bodens. Dies ist die SubCurve mc1_bot_groove, sie ist das Teilstück vom Kurvenanfang (t = 0) von mc1_bot bis zu Bead e14.
Damit sind nun alle Mcs für den neuen Boden bestimmt und es kann die C-spline Lofted Surface bottom_grooved erzeugt werden.
Für den Flächenstreifen vom Rand des multi-konkaven Bodens bis zur Bodenkontur (glatter Boden) werden mit den Beads e14 bis e64 auf ihren Mcs entsprechende SubCurves für das verbleibende Kurvenstück bis t = 1 gebildet. Mit diesen SubCurves wird dann die C-spline Lofted Surface bottom_flat generiert.
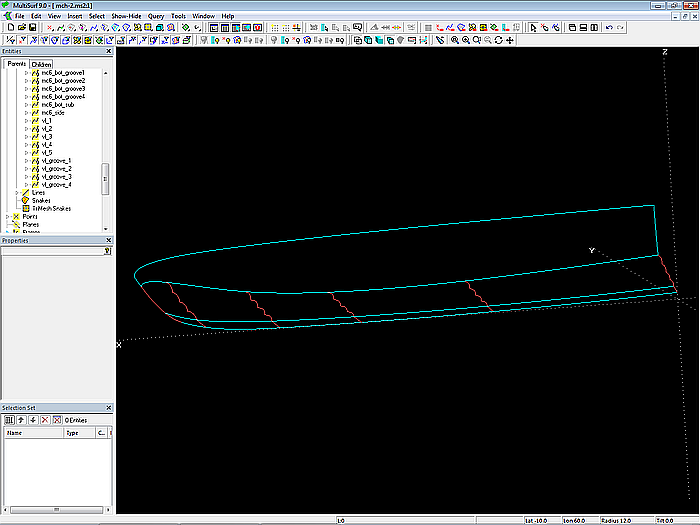
Modell mch-1.ms2 – Mcs für multi-konkaven und glatten Boden
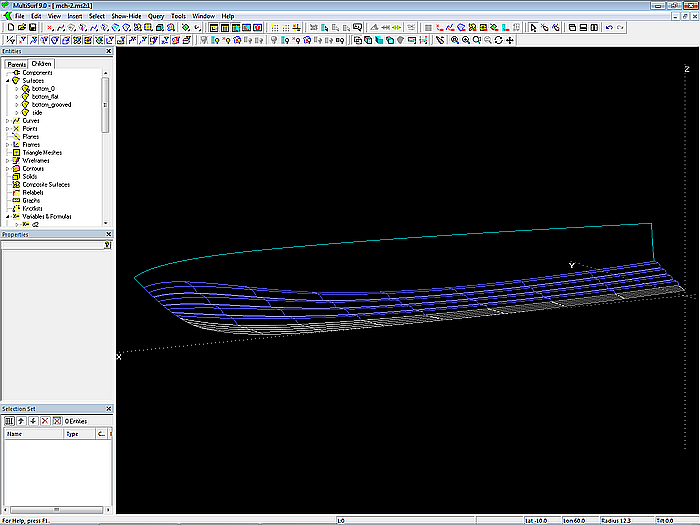
Modell mch-1.ms2 – multi-konkaver und glatter Boden (C-spline Lofted Surfaces bottom_grooved und bottom_flat)
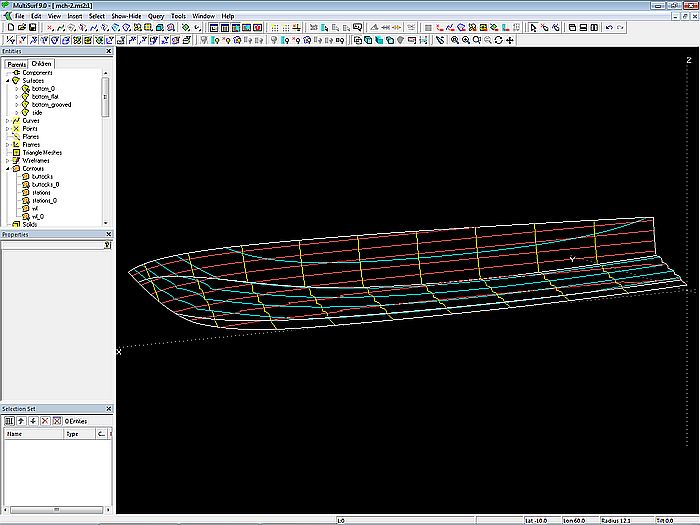
Modell mch-1.ms2 – Motorboot-Rumpf mit multi-konkavem Boden
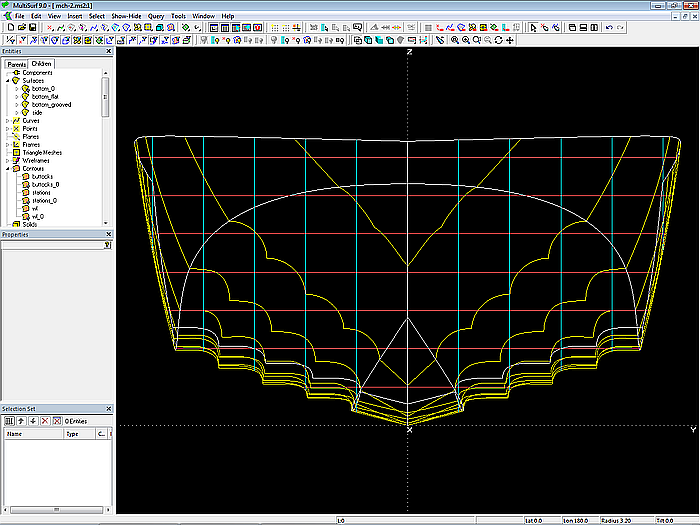
Modell mch-1.ms2 – Motorboot-Rumpf mit multi-konkavem Boden
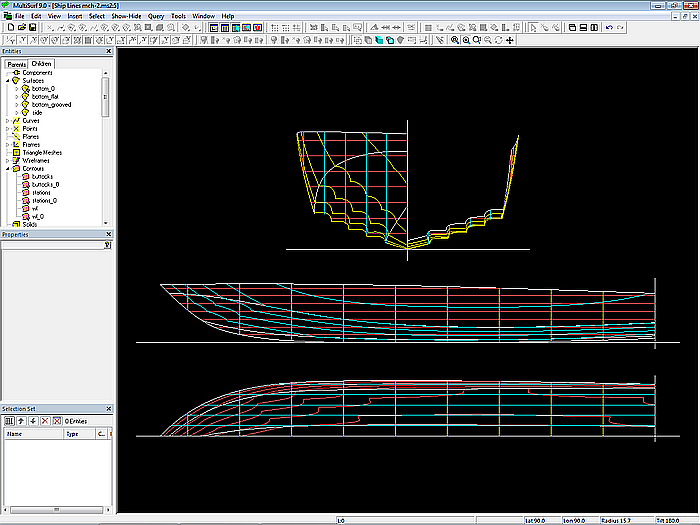
Modell mch-1.ms2 – Motorboot-Rumpf mit multi-konkavem Boden (Ship Lines view)
Im vorgestellten Modell mch-1.ms2 werden die Mcs für den multi-konkaven Boden mit Hilfe von Variablen und Formeln nach bestimmten Regeln auf Basis der Mcs des Standard-Bodens generiert. Die Form der Einbuchtungen ist geometrisch ähnlich. Durch Ändern der Variablenwerte c1, c2, c3 und c4 läßt sich die Querschnittsform modifizieren. Bei Änderungen der Basis-Rumpfform oder der Breite des glatten Bodens ändern sich die Einkehlungen im Boden automatisch mit, behalten aber ihre Formmerkmale (Kurvenstart horizontal, gerades Teilstück, Kurvenende vertikal).
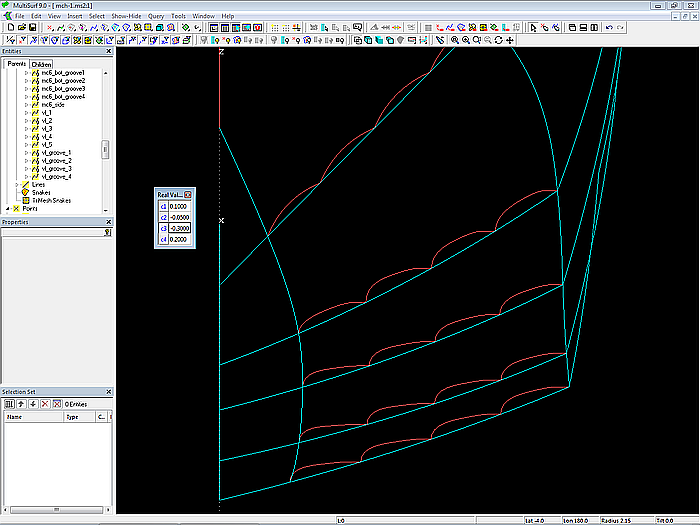
Modell mch-1.ms2 – die Form der Mcs für den multi-konkaven Boden läßt sich über Variablen ändern.
Im Modell mch-1.ms2 wird angenommen, dass sich die Größe der Variablen c1 bis c4 über die Länge nicht ändert, das heißt, sie sind für alle Mcs gleich. Durch entsprechende Formeln kann auch eine Längenabhängigkeit eingebaut werden. So dass beispielsweise die Länge des geraden Teilstücks der Einkehlung von vorn nach achtern zunimmt.
Andere geometrisch ähnliche Querschnittsformen lassen sich durch andere Regeln erzielen.
Masterkurven – Freiform-Ansatz
Man kann auch einen Freiform-Ansatz wählen. Dieser wird in Modell mch-freeform.ms2 beschrieben. Seite und Basisfläche des Bodens sind die gleichen wie in Modell mch-1.ms2.
Die Einbuchtungen sind B-spline Curves, auch die an Mc2. Die Cps sind freie Punkte, sie haben keinen Formelbezug. Durch manuelles Verschieben der Cps kann die Querschnittsform des multi-konkaven Bodens den Entwurfsvorstellungen angepaßt werden.
Um einen in Längsrichtung strakenden Verlauf der Einkehlungen zu erreichen, werden korrespondierende Cps durch C-spline Curves verbunden. Straken diese, sind auch die Einkehlungen strakend.
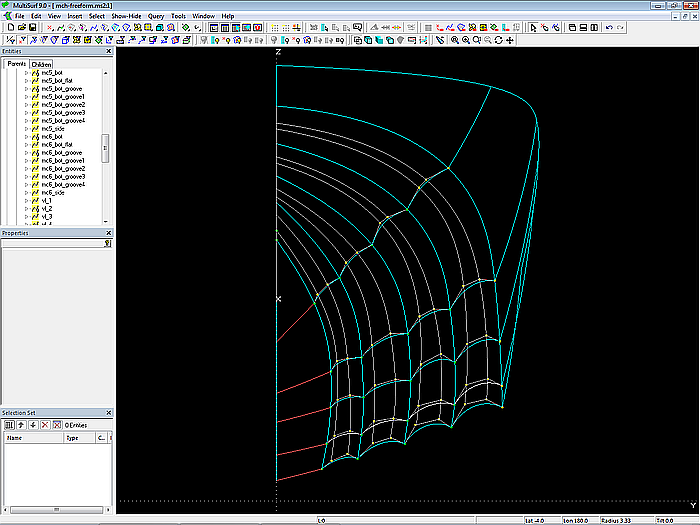
Modell mch-freeform.ms2 – Masterkurven und Strakhilfskurven der multi-konkaven Bodenfläche
Gibt es genaue Vorstellungen über die Querschnittsform der einzelnen Einkehlungen und lassen sich diese nicht durch geometrische Regeln bewerkstelligen, ist der Freiform-Ansatz vorzuziehen. Dann gibt es keine Einschränkungen in der Gestaltung. Allerdings nimmt das Positionieren einer erheblichen Anzahl freier Punkte bei gleichzeitig strakender Form beträchtliche Zeit in Anspruch. Wird die Basisgeometrie des Rumpfes geändert, muß die ganze Arbeit wiederholt werden.
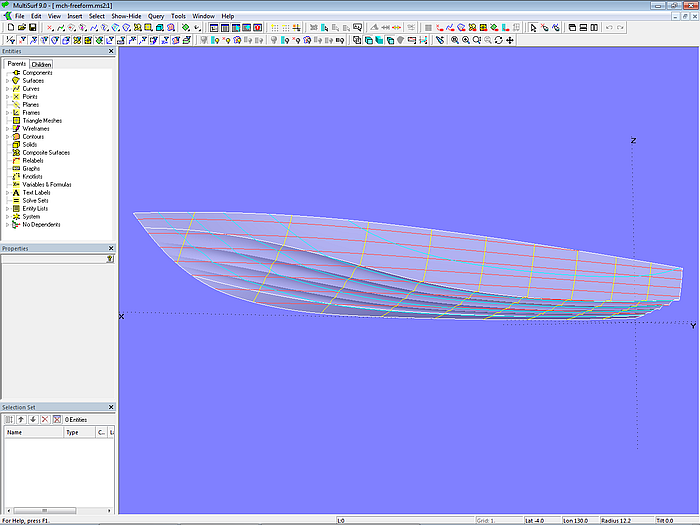
Modell mch-freeform.ms2
3 Swath-Schiff: Übergang Auftriebskörper–Stützfläche
Bei der in diesem Abschnitt beschriebenen Entwurfsaufgabe geht es um die Konstruktion einer Übergangsfläche zwischen zwei aneinanderstoßenden Flächen. Zunächst werden allgemeine Lösungsansätze vorgestellt. Anschließend wird eine Anwendung am Beispiel eines Swath-Schiffes gezeigt.
Stoßen zwei Flächen aneinander, kann aus diversen Gründen ein allmählicher Übergang zwischen beiden Flächen gewünscht werden. In Tutorium 18, Formmerkmale – über Besonderheiten der Geometrie von Rumpf, Deck und Kiel wird im Abschnitt „Abrundungen“ an Hand mehrerer Beispiele gezeigt, wie sich entsprechende Aus- und Abrundungen modellieren lassen. Im vorliegenden Fall soll der Übergang zwischen Stützfläche und Tauchkörper wie bei einem Swath-Schiff betrachtet werden.
3.1 Formmerkmale
Geometrischen Merkmale der Übergangsfläche:
• tangentialer Einlauf in beide Randflächen
• Form veränderbar
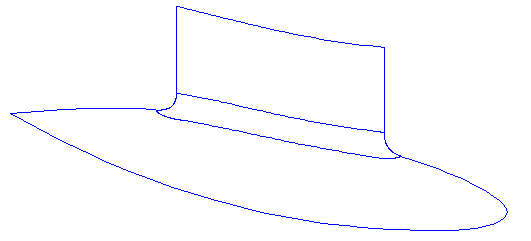
3.2 Basismodell
Das Modell base.ms2 ist das Basis-Modell für die weitere Erörterung. Es enthält die beiden Flächen pod_0 und strut_0. Dabei ist aus Gründen der Übersichtlichkeit pod_0 nur ein Teil des Auftriebskörpers.
Die Fläche pod_0 ist eine B-spline Lofted Surface mit 6 Mcs. Dabei ist Mc1 durch Point mc1_pod gegeben, und Mc6 durch Point mc6_pod; sie sind keine Kurven mit endlicher Länge, sondern zu einem Punkt degenerierte Kurven. Die inneren Mcs sind B-spline Curves mit je 5 Cps und Degree = 3.
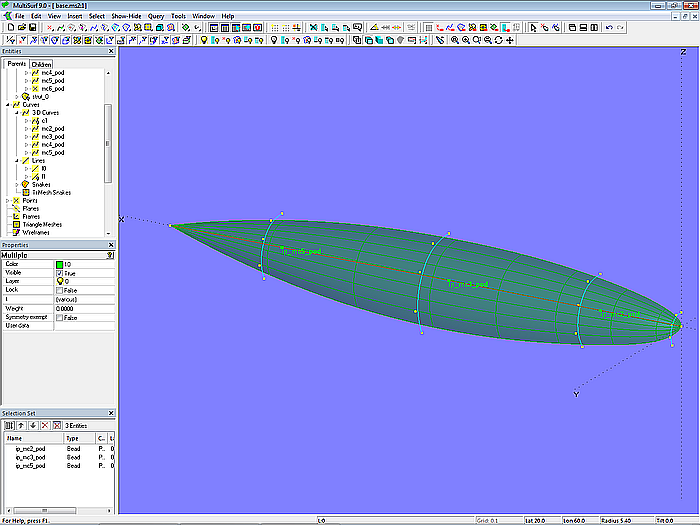
Modell base.ms2 – B-spline Lofted Surface pod_0
Die Cps der inneren Mcs sind Relativpunkte zu Beads auf der Line l0, der Verbindungslinie zwischen Point mc1_pod und Point mc6_pod. Durch diese Beziehung kann der Verlauf der Form in Längsrichtung durch Verschieben der Beads verändert werden.
Basis für die Stützfläche ist die C-spline Curve c1, bestimmt mit 4 Cps; sie beschreibt ihre Wasserlinenform. Diese wird auf pod_0 projeziert als Projected Snake sn1. Zwischen c1 und sn1 ist die Ruled Surface strut_0 aufgespannt. Ihre Vorderkante ist nicht rund wie bei einem Kiel oder Ruder, sondern scharf.
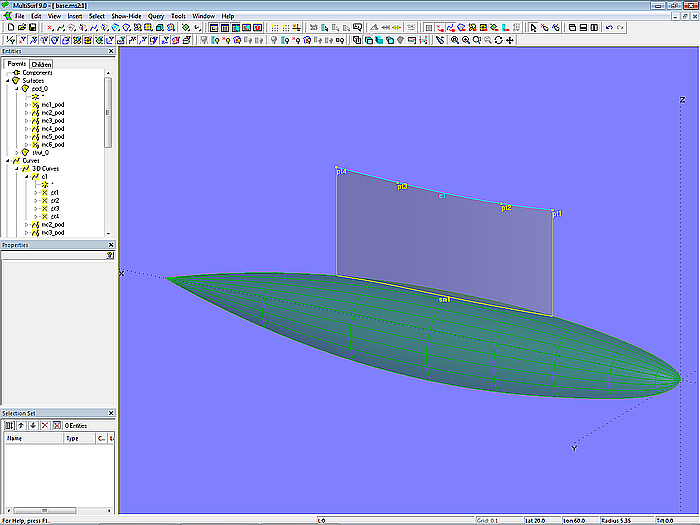
Modell base.ms2 – Ruled Surface strut_0
3.3 Ausrundungsfläche 1 – Rolling Ball Fillet
Eine Ausrundungsmethode für zwei aneinander stoßende Flächen bietet die Flächenart Rolling Ball Fillet. Sie ist der anliegende Teil der Hüllfläche einer Kugel, die zwischen beiden Flächen rollt. Im Modell base_rolling_ball.ms2 ist dies gezeigt.
Eltern eines Rolling Ball Fillets sind die Kurve, entlang der die Kugel rollen soll, die beiden auszurundenden Flächen und der Radius der Kugel. Entsprechend wird im Modell base_rolling_ball.ms2 das Rolling Ball Fillet fillet_0 definiert mit der Projected Snake sn1 sowie den Flächen strut_0 und pod_0. Der Radius ist gesetzt auf 0.15 m.
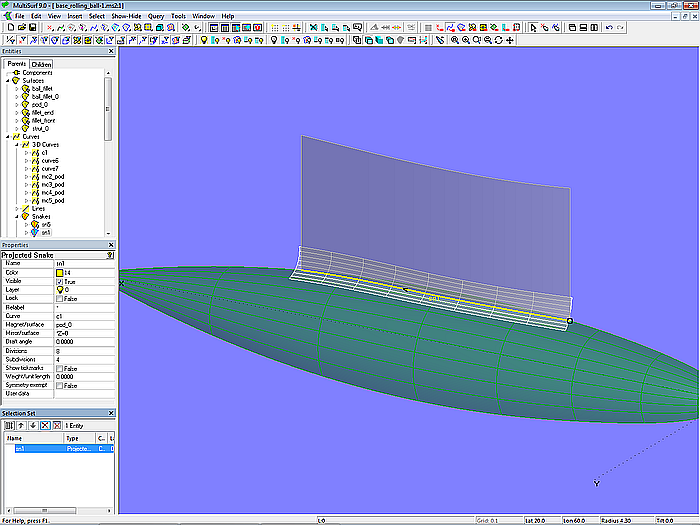
Modell base_roling_ball.ms2 – Rolling Ball Fillet als Ausrundung
An der Vorderkante und an der Hinterkante ist auf Grund der Form der Stützfläche die Ausrundung fillet_0 offen. Mit den beiden Tangent Boundary Surfaces fillet_front und fillet_end wird sie geschlossen. Deren Konstruktion soll an Hand der Fläche fillet_front erklärt werden.
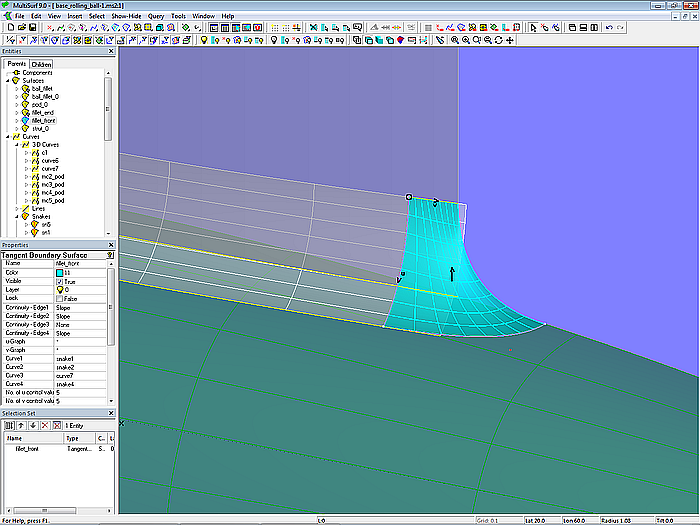
Modell base_rolling_ball.ms2 – Tangent Boundary Surface fillet_front
Das Endstück für die Ausrundung muß an drei Kanten tangential zur angrenzenden Fläche verlaufen, also tangential zu pod_0, zu fillet_0 sowie zu strut_0. Das bedeutet, dass jede dieser Kanten eine Snake auf der entsprechenden Fläche ist.
Beginnen wir mit Snake sn1_front, eine Line Snake auf der Fläche fillet_0 zwischen Ring r1 auf der Oberkante von fillet_0 (EdgeSnake ue_fillet_0) und Ring r2 auf der Unterkante (EdgeSnake bt_fillet_0). Line Snake sn1_front legt also die Größe des Endstücks in Längsrichtung fest.
Snake sn2_front ist eine B-spline Snake auf pod_0, definiert mit Copy Ring r3 auf Projected Snake sn2, Tangent Magnet m1 und Ring r4 auf der Oberkante von pod_0 (EdgeSnake ue_pod_0). Durch die Verwendung des Objekts Tangent Magnet ist die Beziehung fest verankert, dass die Unterkanten von fillet_front (Endstück) und fillet_0 tangential zueinander sind.
Snake sn3_front ist Projected Snake des Teilstücks der Oberkante von fillet_0 von seinem vorderen Ende bis zu Ring r1 (SubSnake sn3).
Abschließend wird als letztes Elternteil der Tangent Boundary Surface fillet_front die Vorderkante durch die B-spline Curve c_front erzeugt.
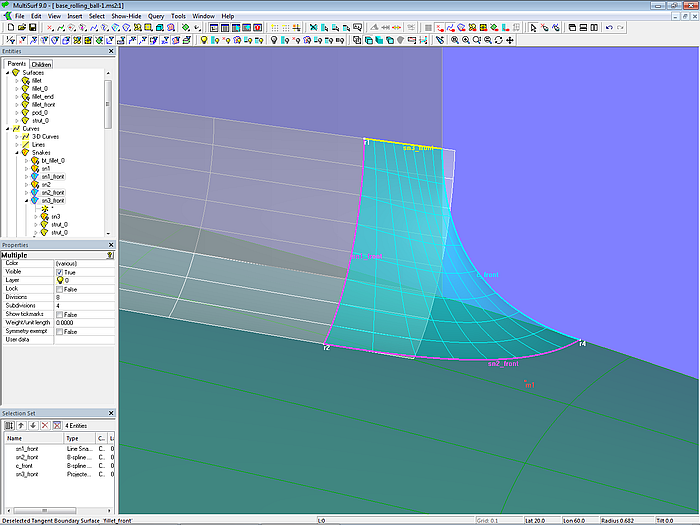
Modell base_rolling_ball.ms2 – Tangent Boundary Surface fillet_front
Analog ist das Endstück der Ausrundung achtern konstruiert.
Abschließend werden die von der Ausrundung nicht überdeckten Flächenteile der Stütze und des Auftriebskörpers bestimmt (Trimmed Surfaces strut und pod). Das Teilstück der Ausrundung zwischen den Enden ist als SubSurface fillet erzeugt.
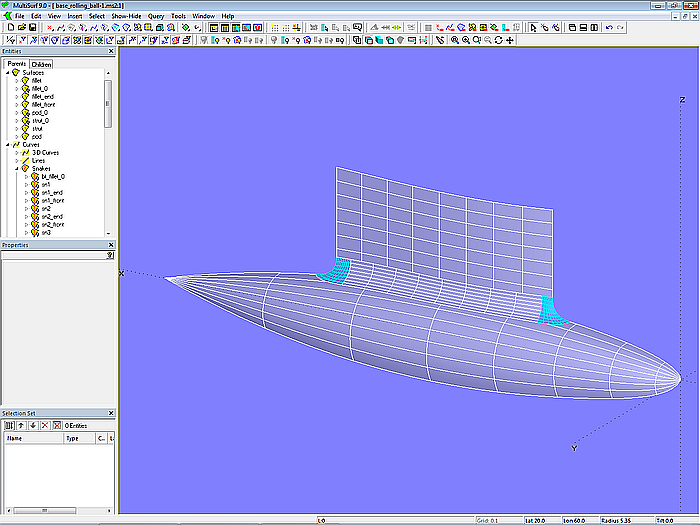
Modell base_rolling_ball.ms2 – Ausrundung zwischen Stützfläche und Auftriebskörper mit Rolling Ball Fillet (Radius konstant)
Bei näherer Betrachtung fällt jedoch auf, dass Schnitte durch die Ausrundung nicht harmonisch verlaufen.
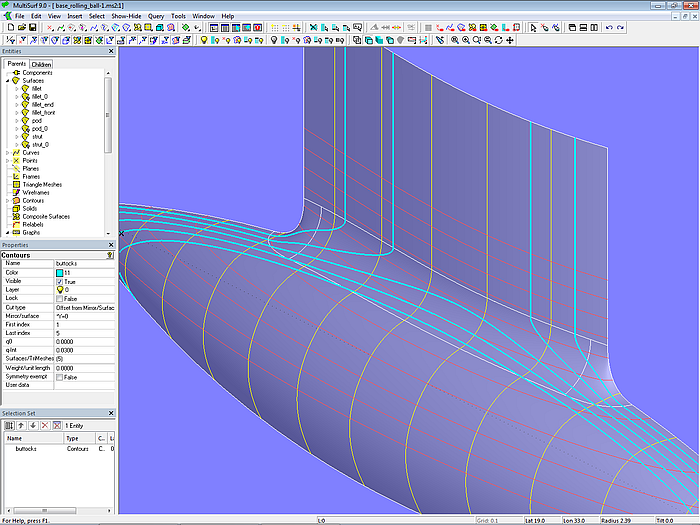
Modell base_rolling_ball.ms2 – unharmonischer Verlauf der Schnitte (Rolling Ball Fillet mit konstantem Radius)
Dies läßt sich beheben, wenn der Radius der Ausrundung sich über der Länge ändert. Für diesen Zweck verfügt die Flächenart Rolling Ball Fillet über die Eigenschaft „Graph“. Wird ein Rolling Ball Fillet in ein Modell eingefügt, ist als Vorgabe das Systemobjekt „*“ eingetragen. Dies bedeutet, dass der Radius über der Länge der Ausrundungsfläche konstant bleiben soll. Soll sich der Radius ändern, muß für die Eigenschaft „Graph“ ein Graph-Objekt verwendet werden. Im Modell base_rolling_ball.ms2 gibt es bereits hierfür den B-spline Graph graph1. Wird nun graph1 statt der Vorgabe „*“ eingesetzt, ist der Kugelradius variabel.
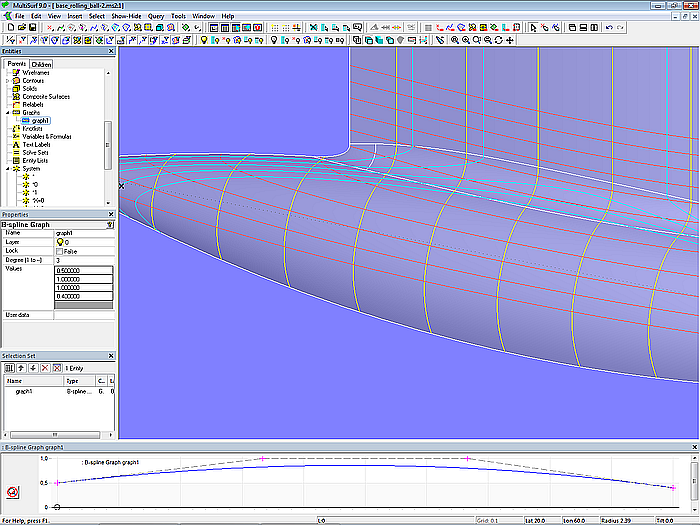
Modell base_rolling_ball.ms2 – Rolling Ball Fillet mit B-spline Graph graph1; der Ausrundungsradius variiert über der Länge.
3.4 Ausrundungsfläche 2 – Blend Surface
Im Modell base_blend_surface.ms2 wird für die Ausrundung eine Fläche vom Typ Blend Surface verwendet.
Für eine Blend Surface werden 4 Supports benötigt: zwei Snakes auf Fläche 1 (strut_0) und zwei Snakes auf Fläche 2 (pod_0). Line Snake sn2 auf strut_0 legt den Beginn der Ausrundung fest. Die andere Snake auf Fläche 1 ist ihre Unterkante (Edge Snake bt_strut_0). Projected Snake sn1 ist die eine Snake auf Fläche 2, die andere ist die B-spline Snake sn4, erzeugt mit 5 Kontrollmagneten. Sie definiert das Ende der Ausrundung auf pod_0. Mit diesen 4 Snakes ist die Blend Surface fillet bestimmt.
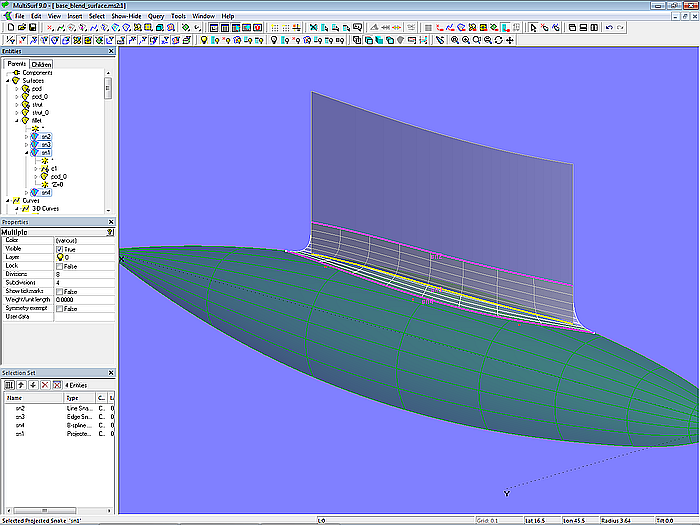
Modell base_blend_surface.ms2 – Ausrundung mit Blend Surface
Mit der Eigenschaft „Type“ der Blend Surface läßt sich der Verlauf der Ausrundung in Querrichtung beeinflussen. Für Type = 1 ist der Randanschluß tangential, für Type = 2 sowohl tangential also auch krümmungstetig; die Ausrundung verläuft enger.
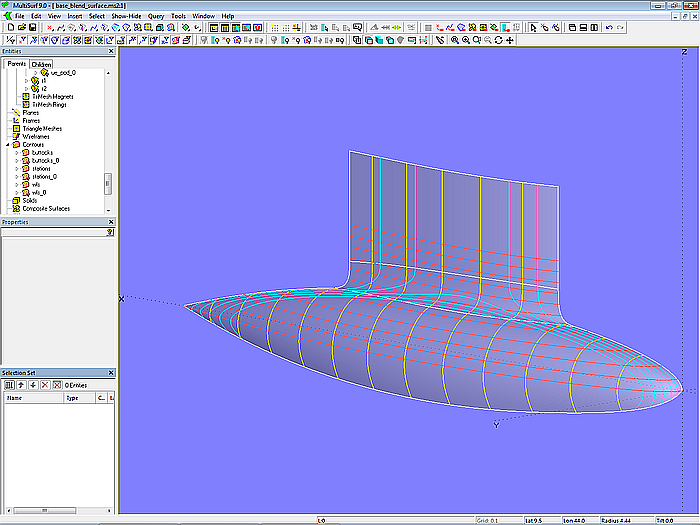
Modell base_blend_surface.ms2 – Ausrundung mit Blend Surface
3.5 Anwendungsfall – Swath-Schiff
Nach diesen Vorbereitungen zum Thema Ausrundung wollen wir uns der eigentlichen Entwurfsaufgabe zuwenden, die Konstruktion eines allmählichen Übergangs zwischen Stützfläche und Auftriebskörper bei einem Swath-Schiff. Dies soll beispielhaft an Hand des Modells swath-1.ms2 gezeigt werden.
Die englische Bezeichnung Small Waterplane Area Twin Hull (SWATH) bedeutet auf Deutsch Doppelrumpf mit geringer Wasserlinienfläche. Der über Wasser angeordnete Rumpf mit Plattform ist über schmale Stege oder Stützen mit den beiden stromlinienförmigen Auftriebskörpern unter der Wasseroberfläche verbunden.
Anmerkungen zum Modell
Modell-Einstellungen (Tools/ Options/...)
.../ Model Units: Meters / Kilograms
.../ Performance: Decimal places = 4; Divisions multiplier = 2
.../ Dragging: Nudge amount = 0.01 [m]
Koordinatensystem
Statt des globalen Koordinatensystems wird als Koordinatensystem des Modells der 3-point Frame frame1 verwendet. Dadurch kann der gesamte Rumpf einfach an die gewünschte Breitenposition verschoben werden.
Mittelebene Rumpf
Die Mittelebene des Rumpfes ist die 2-point Plane plane1.
Modell-Aufbau
Die Modellgeometrie läßt sich einteilen in Aussen- und Innenflächen Rumpf (Semi Hull), Plattform, den vollgetauchten Auftriebskörper sowie die Stützfläche zwischen Unterseite Rumpf und Auftriebskörper, die die Wasseroberfläche durchstößt.
Rumpfflächen
Die Aussen- und Innenflächen des Rumpfes sowie die Plattform werden durch Ruled Surfaces gebildet, die entlang gemeinsamer Längskanten mit einem Knick aneinander stoßen (Rumpf in Knickspantform). Sie werden gestützt von B-spline-Masterkurven mit 5 beziehungsweise 6 Kontrollpunkten.
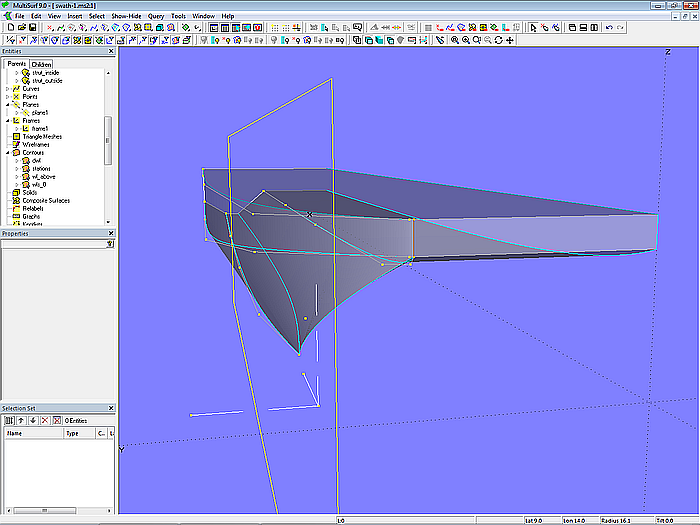
Modell swath-1.ms2 – Masterkurven der Flächen für Rumpf und Plattform
Auftriebskörper und Stützfläche
Im Gegensatz zu den einleitenden Beispielen oben wird der Auftriebskörper durch eine Revolution Surface gebildet (hull_pod_0). Ihr Meridian ist die B-spline Curve c1; Drehwinkel = 360°).
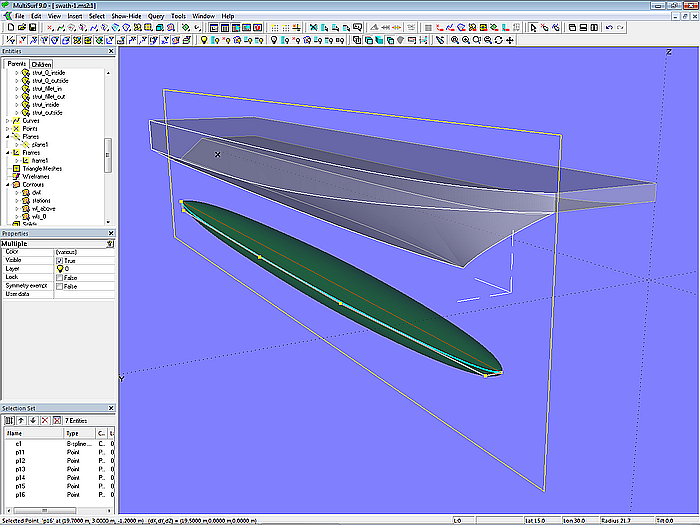
Modell swath-1.ms2 – der vollgetauchte Auftriebskörper ist eine Revolution Surface.
Die Aussenfläche der Stütze zwischen Auftriebskörper und Rumpf ist ebenfalls eine Ruled Surface (strut_0_outside), aufgespannt zwischen B-spline Curve c2 und deren Projektion auf die Revolution Surface hull_pod_0 (Projected Snake sn1_out).
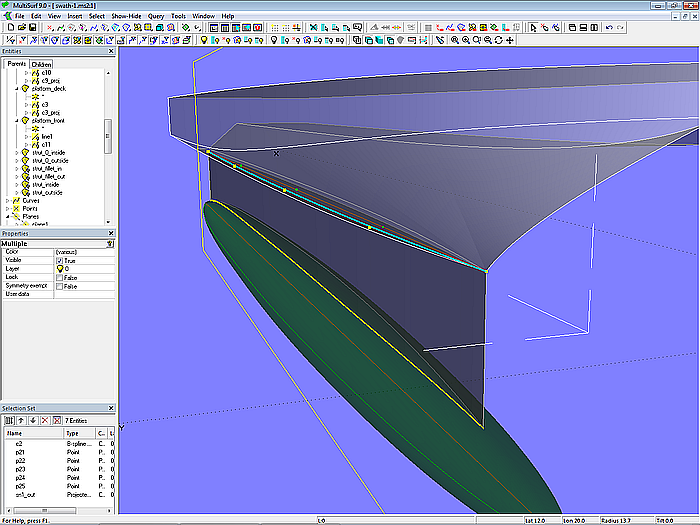
Modell swath-1.ms2 – Stützfläche zwischen Auftriebskörper und Rumpf als Ruled Surface
Die Innenfläche der Stütze (strut_0_inside) ist eine Mirrored Surface. Durch diese Beziehung werden Änderungen an der Form der Aussenseite automatisch auf die Innenseite übertragen.
Übergang Auftriebskörper–Stützfläche
Als Fläche für den Übergang zwischen Auftriebskörper und Stütze wird eine Blend Surface gewählt. Für ihre Definition sind 4 Snakes erforderlich. Snake 1 auf der Stützfläche ist Line Snake sn2_out zwischen Ring r1 (Vorderkante Stütze) und Ring r2 (Hinterkante Stütze). Sie bestimmt den Beginn der Ausrundung. Snake 2 auf der Stützfläche ist ihre Unterkante (Edge Snake sn3_out). Snake 3 liegt auf dem Auftriebskörper als Projected Snake sn1_out. Snake 4 beschreibt das Ende der Ausrundung auf dem Auftriebskörper, dies ist die B-spline Snake sn4_out, definiert mit 5 Cps.
Mit diesen 4 Snakes wird dann die Blend Surface strut_fillet_out erzeugt. Für die Ausrundung auf der Innenseite der Stützfläche wird sie an der Mittelebene plane1 gespiegelt (Mirrored Surface strut_fillet_in).
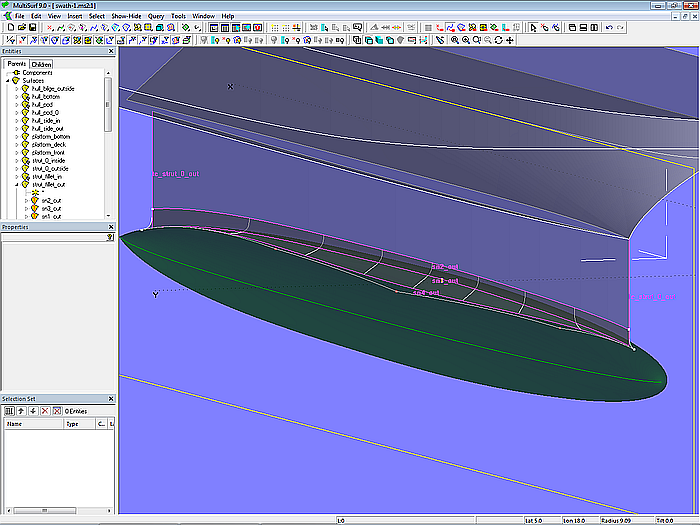
Modell swath-1.ms2 – Ausrundung zwischen Stützfläche und Auftriebskörper als Blend Surface
Abschließend werden die von der Ausrundung nicht überdeckten Flächenteile der Stütze (Trimmed Surfaces strut_outside und strut_inside) und des Auftriebskörpers (hull_pod) bestimmt.
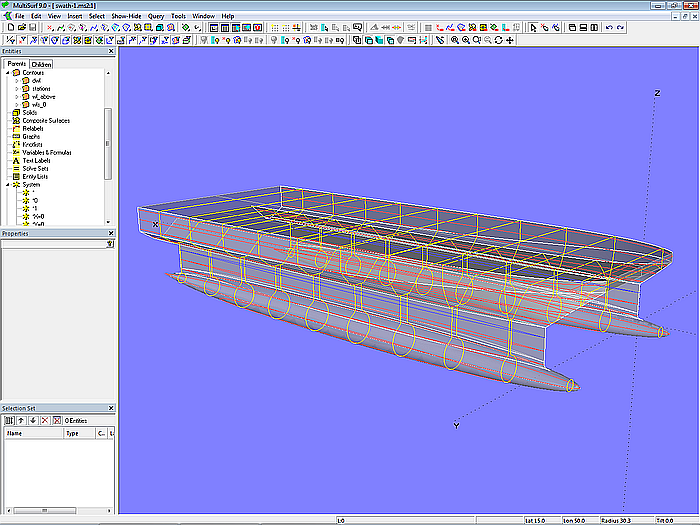
Modell swath-1.ms2 – Shaded view
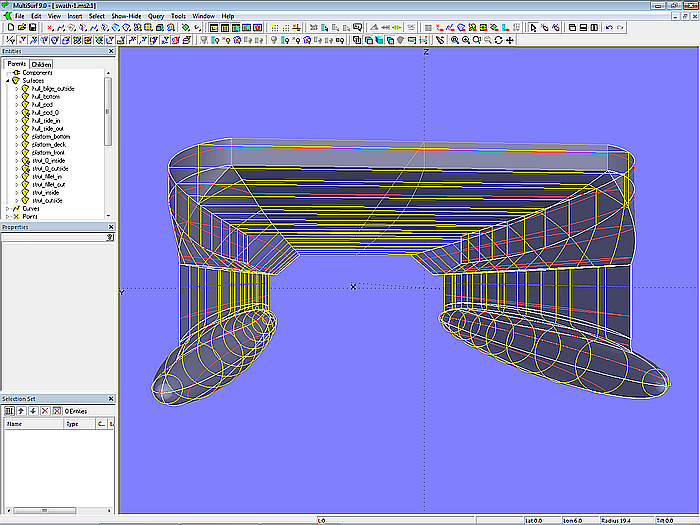
Modell swath-1.ms2 – Shaded view
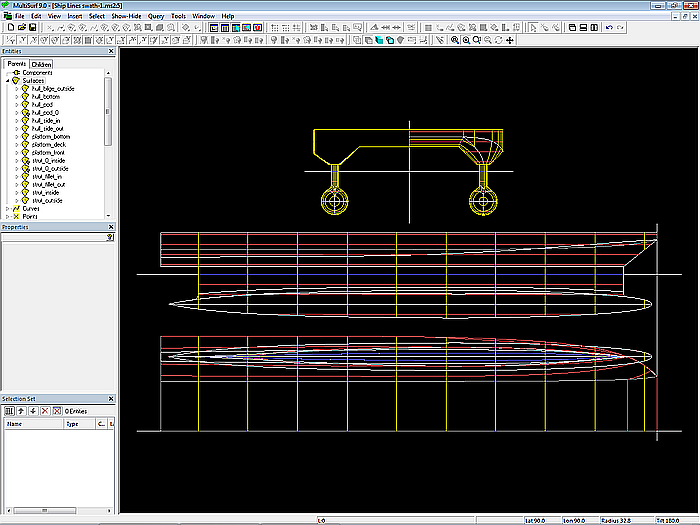
Modell swath-1.ms2 – Ship Lines view
======================================================================================