Über Formeffekte bei Lofted Surfaces
Das Problem mit dem Aufbaudach
von Reinhard Siegel
Juni 2023
Inhalt
Einleitung
1 Das Problem mit dem Aufbaudach
1.1 Lösungsansatz A – zusätzliche Mc
1.2 Lösungsansatz B – Point p43 weit nach außen schieben
1.3 Auf der Suche nach der Ursache
1.4 Lösungsansatz C – mc4 mit Korbbogenform
1.5 Lösungsansatz D – Verschieben von Point p44 nach unten
1.6 Lösungsansatz E – Relabel
1.7 Lösungsansatz F – runde Ecke
1.8 Lösungsansatz F – Tangent Boundary Surface
2 Formeffekte bei Rümpfen
2.1 Rumpf mit eckigem Vorfuß
2.2 Rumpf mit rundem Vorfuß
3 Formeffekte bei Foil Lofted Surface und Arc Lofted Surface
Einleitung
Dieses Tutorium beruht auf dem Hinweis eines MultiSurf-Users, der beim Modellieren eines einfachen Kajütaufbaus für ein Segelboot feststellte, dass Schnitte parallel zur Mittschiffsebene durch das Aufbaudach in der Ecke zwischen Vorder- und Aussenkante des Dachs konkav (hohl) verlaufen.
Ein kastenförmiger Aufbau aus Seite, Front und Dach scheint eine an und für sich einfache Konstruktionsaufgabe zu sein. In Tutorium 13, Decks und Aufbauten, werden hierzu Methoden beschrieben. Der beobachtete Formeffekt verursacht aber manchmal auch Probleme beim Strak von Rumpfflächen. Im vorliegenden Tutorium werden Ursachen und Lösungsmöglichkeiten beschrieben.
Verwendete Abkürzungen:
Cp: Kontrollpunkt, Stützpunkt (control point, support point); synonym verwendet
Mc: Masterkurve, Stützkurve (master curve, support curve); synonym verwendet
cp1, cp2, ...: bezeichnet den 1., 2. ... Punkt in der Liste der Kontrollpunkte einer Kurve. Es ist kein Objektname.
mc1, mc2, ...: bezeichnet die 1., 2. ... Kurve in der Liste der Stützkurven einer Fläche. Es ist kein Objektname.
Im Folgenden werden die MultiSurf-Namen für Punkt-, Kurven- und Flächenarten verwendet. Das ergibt zwar „denglische“ Sätze, soll aber dem Verständnis und der Nachvollziehbarkeit dienen.
1 Das Problem mit dem Aufbaudach
Entwurfsbedingungen
An alle vier Kanten des Aufbaudachs werden bestimmte geometrische Bedingungen gestellt. Die Achterkante des Dachs soll wie ein Korbbogen aussehen. Die Vorderkante soll aber die Form eines Kreisbogens haben, damit die Oberkante der Aufbaufront (= Vorderkante Aufbaudach) ähnlich aussieht wie die Unterkante (Deck mit Kreisbogenbucht). Die Innenkante Aufbaudach soll nach vorne hin abfallen, aber die Außenkante mehr oder weniger horizontal verlaufen beziehungsweise nach vorne hin leicht ansteigen. Desweiteren soll die vordere äußere Dachecke spitz sein, nicht abgerundet.
Ausgangsmodell
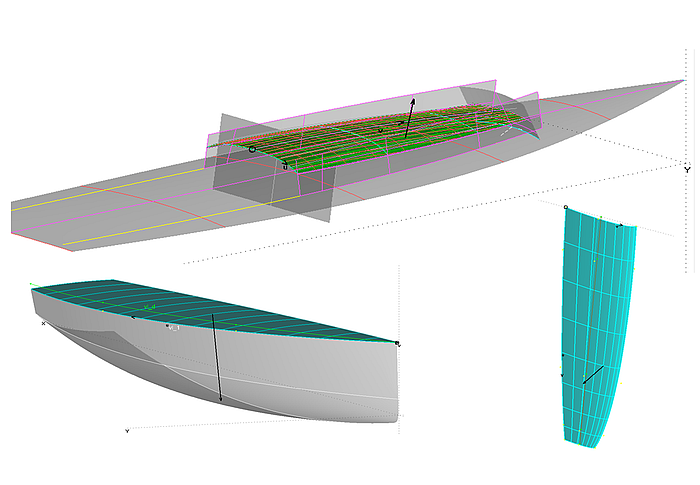
Um die Geometrie auf das Wesentliche zu vereinfachen, wird im Folgenden nur die Dachfläche eines Kajütaufbaus betrachtet. Das Ausgangsmodell ist Modell cabintop-0.ms2. Als Flächentyp wird eine C-spline Lofted Surface gewählt. Die Fläche cabintop wird durch 4 in Querrichtung liegenden B-spline-Masterkurven (Degree = 3) gestützt (mc1, mc2, mc3, mc4). Alle Mcs werden durch je 4 Kontrollpunkte (Cps) bestimmt. Der Korbbogencharakter nimmt von der Hinterkante nach vorne allmählich ab.
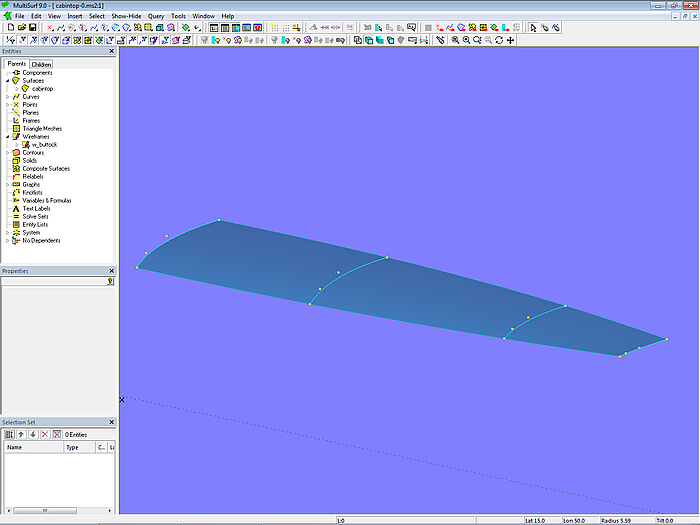
Ausgangsmodell cabintop-0.ms2 – Aufbaudach als C-spline Lofted Surface mit 4 B-spline-Masterkurven
Ausgangsmodell cabintop-0.ms2 – die Korbbogenform der Spanten nimmt zur Vorderkante hin ab.
Obwohl Strakhilfskurven (vl1, vl2, vl3, vl4) auf regelmäßig angeordnete Cps hinweisen, sind Schnitte parallel zur Mittschiffsebene im Bereich der vorderen äußeren Ecke der Dachfläche hohl (konkav).
Ausgangsmodell cabintop-0.ms2 – Schnitte durch das Aufbaudach verlaufen im Bereich der vorderen äußeren Ecke konkav.
Im weiteren Verlauf dieses Tutorials werden verschiedene Ansätze beschrieben, um den Verlauf der Schnitte gleichförmig zu machen.
1.1 Lösungsansatz A – zusätzliche Mc
Um die Fläche nach oben zu drücken, könnte man vorne eine weitere Mc einzufügen. Das wird in Modell cabintop-a.ms2 durch die B-spline Curve mc3a realisiert. Um den Schnittverlauf mit dem Ausgangsmodell cabintop-0.ms2 zu vergleichen, wird außerdem das Wireframe-Objekt w_buttock eingefügt (Farbe weiß).
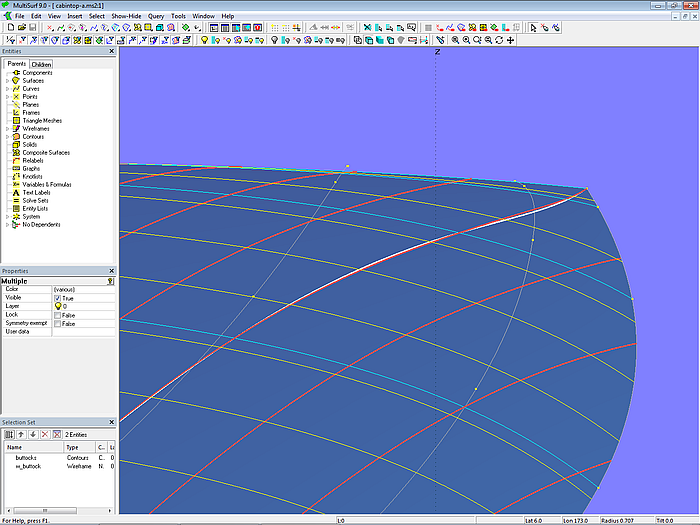
Modell cabintop-a.ms2 – weitere Mc (mc3a) nahe der Vorderkante eingefügt. Die weiße Kurve zeigt den Verlauf des Schnitts im Ausgangsmodell cabintop-0.ms2.
Eine wesentliche Verbesserung bewirkt die zusätzliche Mc nicht. Man kann cp3 der neuen Mc (mc3a) verschieben, wie man will, der konkave Verlauf des Schnitts durch den Eckpunkt verschwindet nicht.
Allerdings kann er etwas reduziert werden, wenn cp3 (Point p43) an der vorderen Mc (mc4) nach außen geschoben wird.
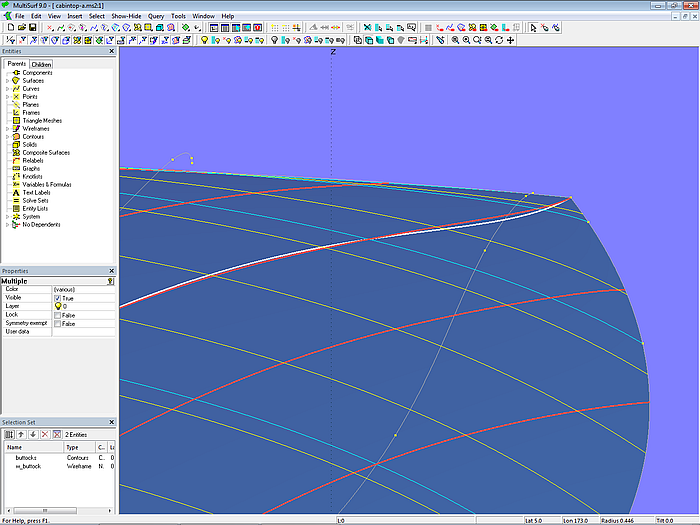
Modell cabintop-a.ms2 – cp3 an der Vorderkante weit nach außen geschoben
1.2 Lösungsansatz B – Point p43 weit nach außen schieben
Überprüfen wir diese Feststellung auch am Ausgangsmodell cabintop-0.ms2 und schieben p43 an mc4 nach außen.
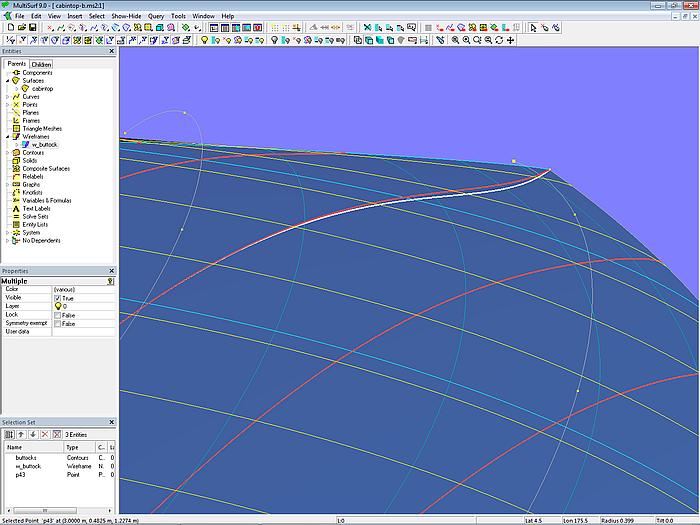
Modell cabintop-b.ms2 – Point p43 weit nach außen geschoben; die Schnittkurve wird weniger hohl.
Auch hier wird der konkave Schnittverlauf abgeschwächt, wenn p43 weiter außen liegt. Allerdings erhält mc4 dadurch eine Korbbogenform.
1.3 Auf der Suche nach der Ursache
Versuchen wir herauszufinden, was den hohlen Verlauf der Schnittkurven verursacht. Dazu wird im Ausgangsmodell cabintop-0.ms2 mit dem Bead bead1 die SubCurve mc3_sub als Teilstück von mc3 erzeugt. Und analog mit dem Bead bead2 die SubCurve mc4_sub als Teilstück von mc4. Mit beiden Kurven wird im Bereich der Ecke nun mit der Ruled Surface patch ein kleines Flächenstück eingefügt. Dies ist Modell cabintop_patch.ms2.
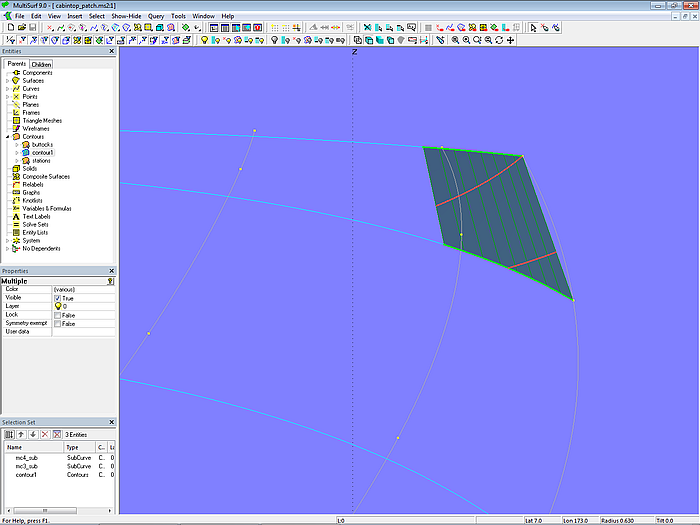
Modell cabintop_patch.ms2 – Flächenbereich in der Ecke angenähert durch Ruled Surface patch
Auch hier sind die Schnitte hohl.
Was auffallend ist: beide Stützkurven (mc3_sub und mc4_sub) der Ruled Surface patch verlaufen sehr verdreht zueinander.
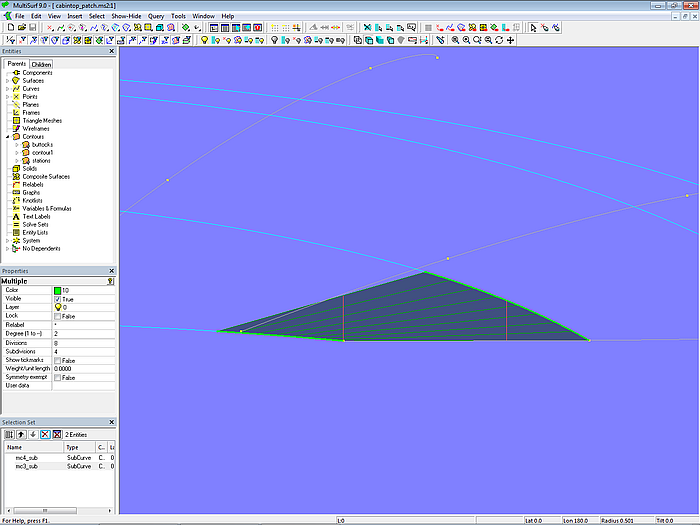
Modell cabintop_patch.ms2 – die Stützkurven der Ruled Surface patch sind stark verwunden.
Verwindung
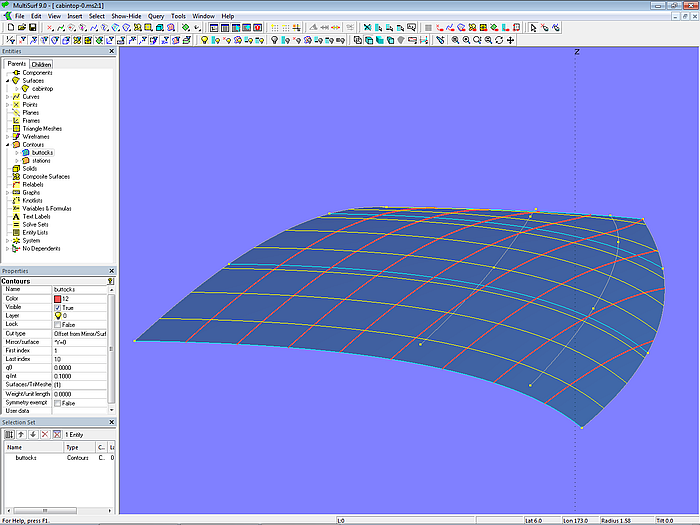
Um herauszufinden, welche Rolle die Verwindung korrespondierender Teilbereiche der Mcs für den Verlauf der Schnitte spielt, wird jede Mc ohne die beiden inneren Cps (cp2, cp3) definiert. Das Ergebnis zeigt Modell cabintop_twist-1.ms2. Innenkante und Aussenkante sind unverändert, die Spanten sind gerade.
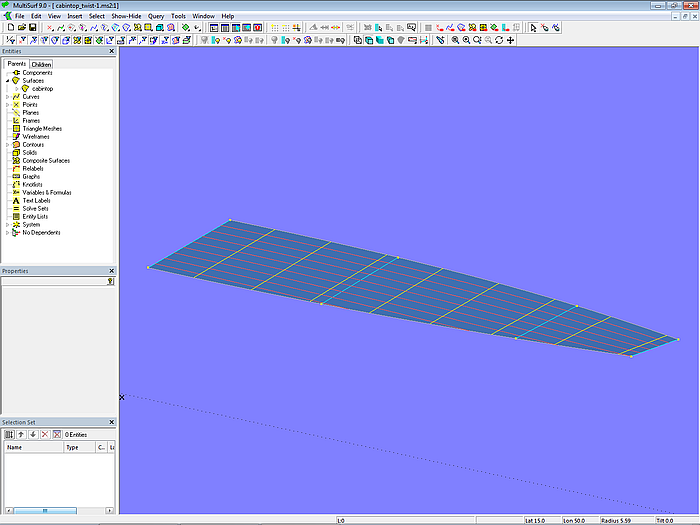
Modell cabintop_twist-1.ms2 – C-spline Lofted Surface mit geraden Mcs
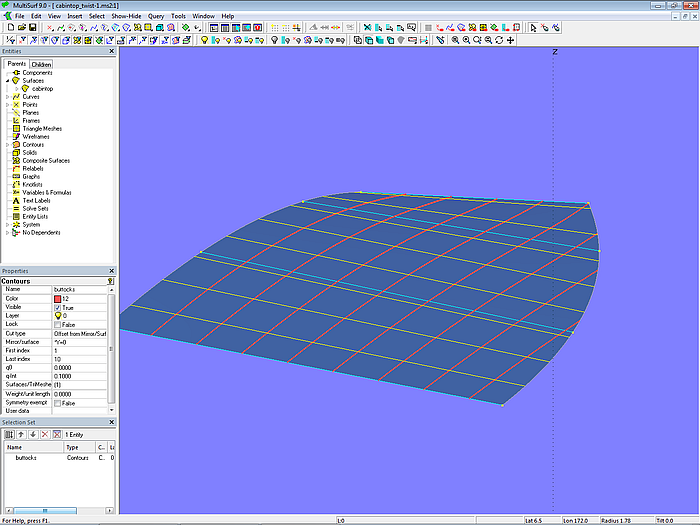
Modell cabintop_twist-1.ms2 – Verlauf der Schnitte parallel zur Mittschiffsebene
In der Nähe der Mittschiffsebene verlaufen die Schnitte konvex, nach aussen hin werden sie im vorderen Bereich konkav gekrümmt.
Vereinfachen wir das Modell noch weiter. Lediglich mc1 und mc4 sollen die Fläche stützen. Dies ist in Modell cabintop_twist-2.ms2 gezeigt. Innen- und Aussenkante sind gerade. Die C-spline Lofted Surface stimmt jetzt mit einer Ruled Surface überein. Zusätzlich legen wir noch die 3-point Plane plane1 durch die beiden hinteren Eckpunkte (p11, p14) und den vorderen inneren Eckpunkt (p41) und projezieren p44 darauf als Projected Point pt1.
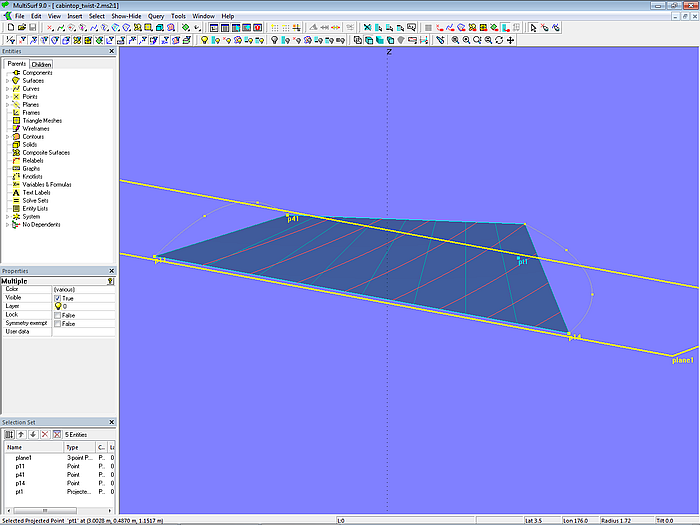
Modell cabintop_twist-2.ms2 – Fläche nur durch mc1 und mc4 gestützt
Verschieben wir nun Point p44 ausschließlich in Z-Richtung und betrachten die Auswirkung auf den Schnittverlauf.
Liegt p44 unterhalb dieser Ebene, sind die Schnitte konvex.
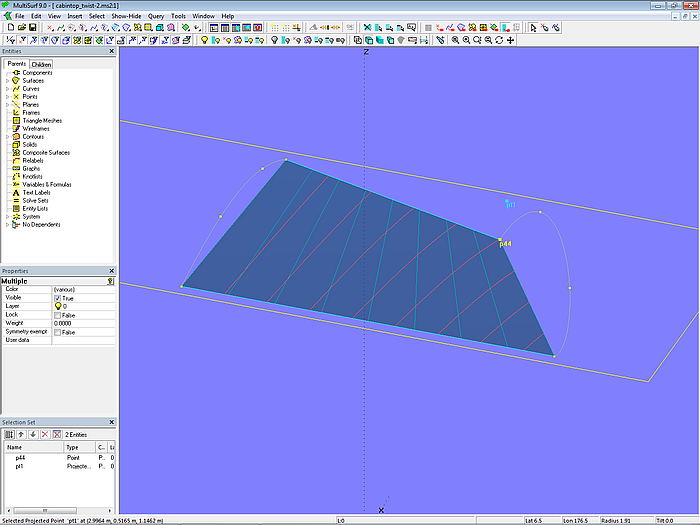
Modell cabintop_twist-2.ms2 – liegt Point p44 unter der Ebene plane1, verlaufen die Schnitte konvex.
Liegt p44 in der Ebene, sind sie gerade.
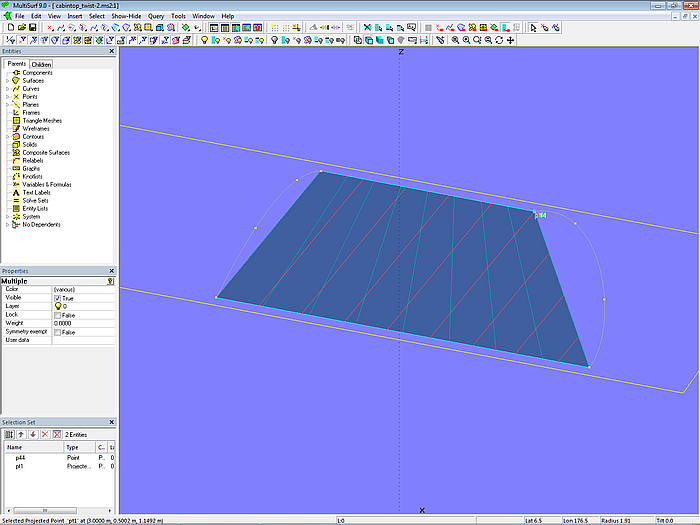
Modell cabintop_twist-2.ms2 – liegt Point p44 in der Ebene plane1, sind die Schnitte gerade.
Liegt p44 über der Ebene, sind die Schnitte konkav.
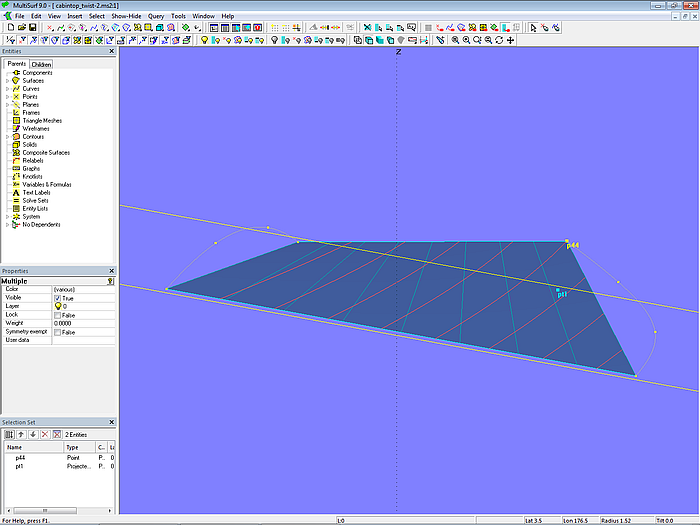
Modell cabintop_twist-2.ms2 – liegt Point p44 über der Ebene plane1, verlaufen die Schnitte hohl.
Fazit: das Problem der hohl verlaufenden Schnitte im Bereich der vorderen äußeren Ecke der C-spline Lofted Surface cabintop im Ausgangsmodell cabintop-0.ms2 wird durch die Verwindung der Stützkurven verursacht. Je weiter die „Beplankung“ der Masterkurven mit den „Lofting Curves“ zum äußeren Rand und damit in die Ecke geht, sind die Teilbereiche der beiden vorderen Mcs (mc3, mc4) immer mehr zueinander verdreht.
Es sei betont, dass die konkaven Schnitte kein Defizit der C-spline Lofted Surface sind. Sie resultieren aus der Verwindung der Stützkurven, die ihrerseits direkte Folge der Entwurfsforderungen ist.
Welche Lösungsmöglichkeiten folgen daraus?
1.4 Lösungsansatz C – mc4 mit Korbbogen
Man gibt die Entwurfsbedingung auf, dass die vordere Mc (mc4) keinen Korbbogenverlauf hat. Point p43 wird weiter nach außen geschoben und sein Koordinatenwert dz gleich dz von Point p41 gesetzt. Dies ist Modell cabintop-c.ms2.
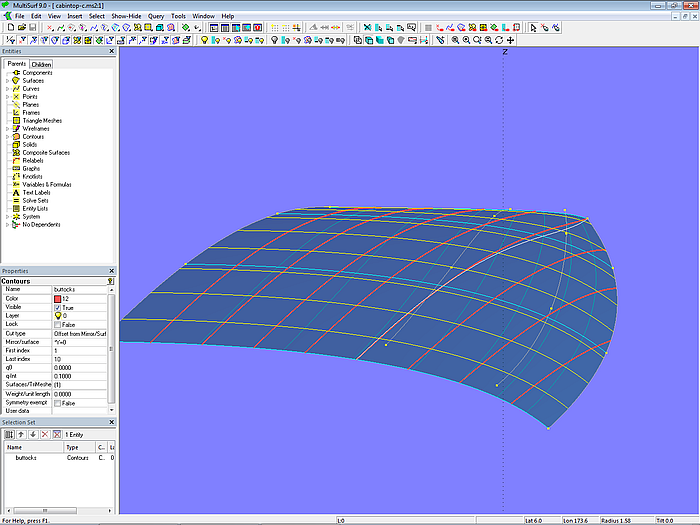
Modell cabintop-c.ms2 – alle Mcs haben einen korbbogenförmigen Verlauf. Die Schnitte sind nicht mehr hohl.
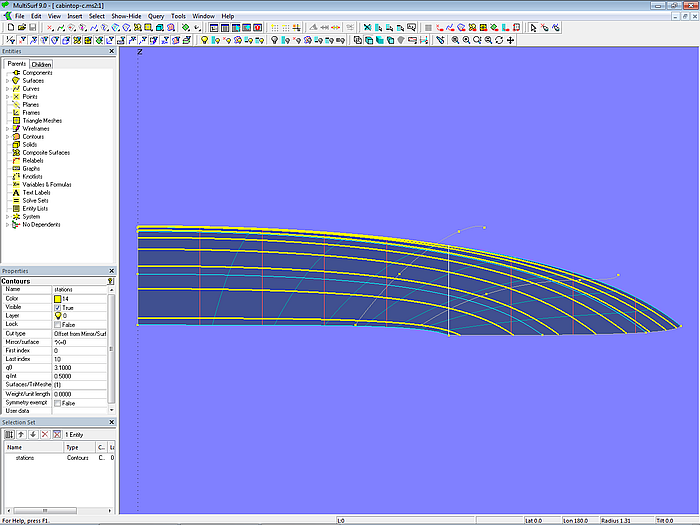
Modell cabintop-c.ms2 – Spantform bei Korbbogen-Mcs
1.5 Lösungsansatz D – Verschieben von Point p44 nach unten
Wie an Hand des stark vereinfachenden Modells cabintop_twist-2.ms2 gezeigt, bewirkt eine Verschiebung von Point p44 nach unten, dass die Schnitte konvex werden. Wenn Point p44 von dz = 1.2233 im Ausgangsmodell cabintop-0.ms2 nach unten zu dz = 1.2033 verschoben wird, reduziert sich dadurch die Verwindung zwischen den Mcs im Bereich der äußeren Ecke und die Schnitte sind nicht mehr hohl.
Dies ist Modell cabintop-d.ms2.
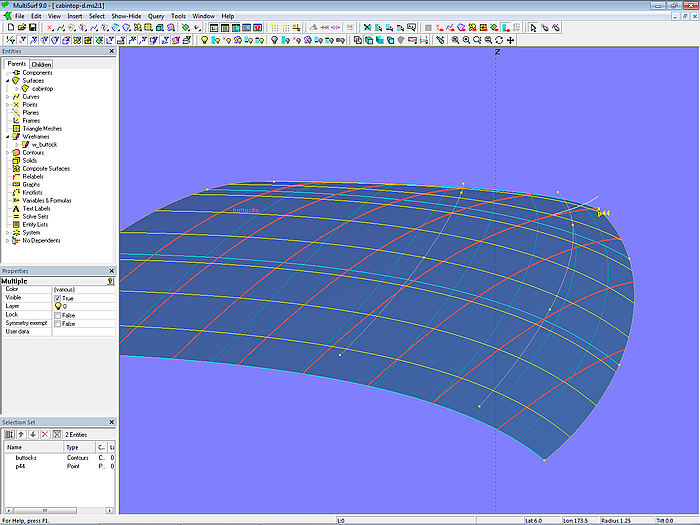
Modell cabintop-d.ms2 – eine Verschiebung von p44 nach unten reduziert die Verwindung.
Auch hier bekommt mc4 einen Korbbogenverlauf.
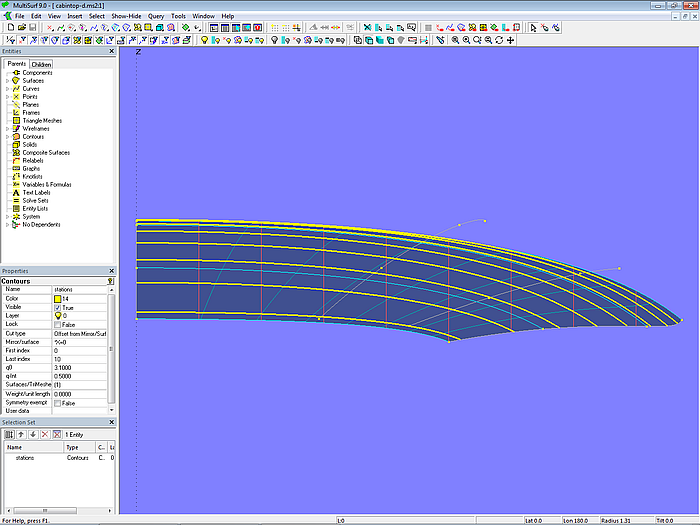
Modell cabintop-d.ms2 – Verwindung reduziert durch Verschieben von p44 nach unten
1.6 Lösungsansatz E – Relabel
Bislang wurde für die Fläche des Aufbaudachs nur die Form ihrer Mcs variiert. Die Fläche ist eine C-spline Lofted Surface, das heißt, die Mcs werden mit C-spline Curves (kubische Splines, Lattenkurven) „beplankt“. Wäre es auch möglich, das Problem des konkaven Schnittverlaufs zu lösen, wenn der Prozess des „Beplankens“ beeinflusst wird?
Dazu einige Erläuterungen vorab.
Parameterverteilung
Kurven in MultiSurf sind parametrische Kurven. Die Koordinaten ihrer Kurvenpunkte sind Funktionen eines Parameters t, der zwischen 0 und 1 variiert. Faßt man t als Zeit auf, dann beschreibt die Kurve den Pfad eines sich bewegenden Punktes. Zu jedem Kurvenpunkt gehört ein Wert des t-Parameters.
Für den Anfang einer Kurve ist der Parameterwert t = 0, für das Ende ist t = 1. Wie die Kurvenpunkte dazwischen verteilt sind (Parameterverteilung) läßt sich anzeigen, wenn man im Properties-Manager bei den Kurveneigenschaften „Show tickmarks“ auf „True“ setzt. Dann werden für ein t-Intervall von 0.1 die entsprechenden Kurvenpunkte markiert (labeln).
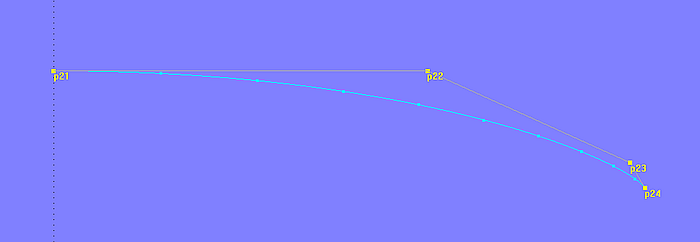
B-spline Curve mit Anzeige der Parameterverteilung für t-Intervall = 0.1.
Natural label
Jede Kurvenart hat eine natürliche Parametrisierung (natural label). Bei einer C-spline Curve liegen die Kurvenpunkte gleichmäßig über die Länge verteilt, bei einer Line liegt der Kurvenpunkt für t = 0.5 auf der Hälfte, für t = 0.75 auf 3/4 der Länge. Bei einer B-spline Curve sind sie ähnlich verteilt wie die Kontrollpunkte – wo diese dicht beieinander angeordnet sind, liegen auch die Kurvenpunkte nah zusammen. Liegen mehrere Cps übereinander, beziehungsweise wird ein Punkt mehrmals in der Liste der Cps verwendet, kann eine Reihe von Kurvenpunkten die gleichen Koordinaten haben, jeweils mit anderem t-Wert.
Relabel
Eine Kurve läßt sich aber auch neu einteilen, den Kurvenpunkten können andere t-Parameterwerte zugewiesen werden (Re-Parametrisierung). So dass zum Beispiel bei einer Line der Kurvenpunkt auf halber Länge nicht den t-Wert = 0.5 hat (natürliches Label), sondern t = 0.75 (Relabel). Dazu gibt es in MultiSurf die Objekte Relabel und SubCurve. Die Kurvenform ändert sich nicht beim Relabeln, auch die Position der Kurvenpunkte bleibt gleich, lediglich der zugehörige t-Parameterwert wird verändert.
Modell relabel.ms2 zeigt am Beispiel einer B-spline Curve und einer Line, wie sich mit SubCurve die Parametrisierung von Kurven ändern läßt. Dazu setzt man einen oder mehrere Beads auf die zu relabelnde Kurve und erzeugt mit diesen und den System-Beads *0 und *1 (Entities Manager/ System) als Control beads eine SubCurve. Wird „Show tickmarks“ eingeschaltet, kann man gut sehen, wie sich die Parameterverteilung mit der Position der Beads ändert.
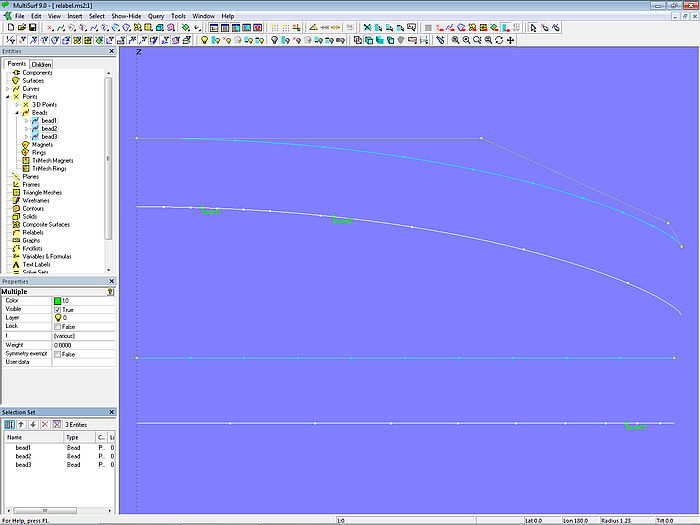
Modell relabel – B-spline Curve und Line mit natürlichem Label und relabelt mit SubCurves
Lofted Surface
Um eine Lofted Surface zu erzeugen, wird zunächst an jeder Mc für den gleichen Parameterwert t der Kurvenpunkt bestimmt. Die resultierende Punkte sind dann die Stützpunkte für die „Lofting Curve“. Der Parameterwert t variiert zwischen 0 und 1, so dass eine Serie von Lofting Curves über die Mcs entsteht, die in ihrer Summe eine Fläche im Raum überstreichen. Je nach Typ der Lofting Curve entsteht eine Arc Lofted Surface, B-spline Lofted Surface, C-spline Lofted Surface, Foil Lofted Surface oder X-spline Lofted Surface. Bei einer C-spline Lofted Surface ist der Vorgang analog zum Bau eines Rumpfes in Leistenbauweise, wo über Mallen eine Serie von Leisten gelegt wird.
Parameterkurven
Der Verlauf der Lofting Curves wird angezeigt, wenn im Properties-Manager in den Eigenschaften einer Lofted Surface „Show u-constant“ auf „True“ gesetzt ist. Dann wird die mit der Eigenschaft „“u-Divisions“ festgelegte Serie von Lofting Curves angezeigt. Diese Kurven werden auch als u-Parameterkurven der Fläche bezeichnet.
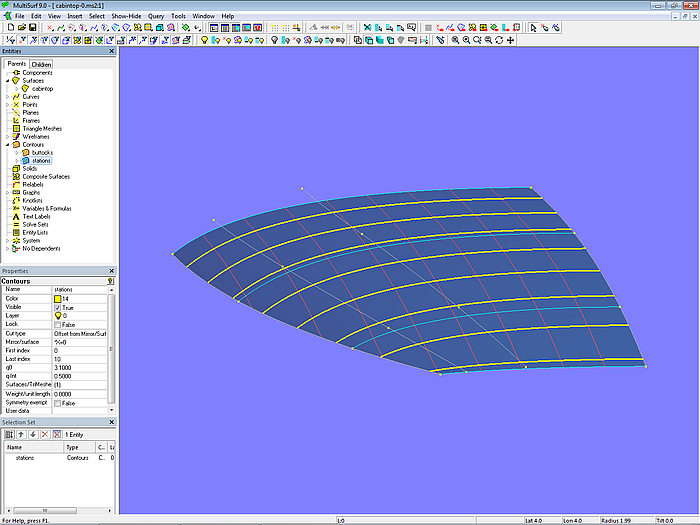
Betrachten wir das Ausgangsmodell cabintop-0.ms2 und lassen uns die Lofting Curves (u-Parameterkurven) anzeigen.
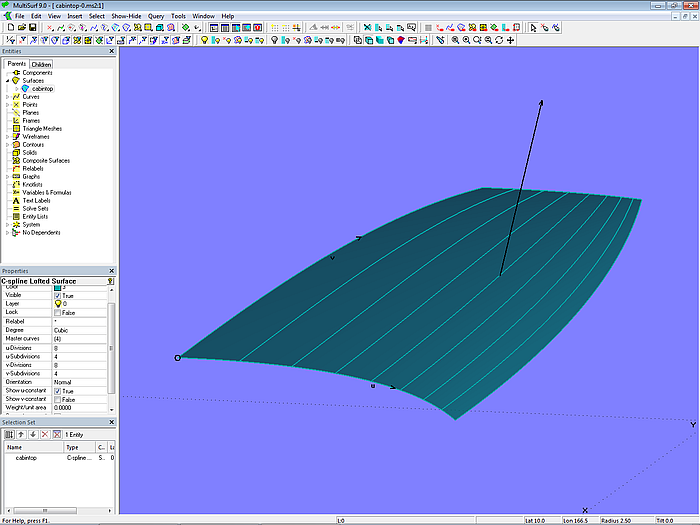
Modell cabintop-0.ms2 – u-Parameterkurven angezeigt mit „Show u-constant“
Die u-Parameterkurven verlaufen regelmäßig. Was daran liegt, dass zum einen die Cps der B-spline-Mcs in Längsrichtung mit Hilfe der Vertexkurven vl1 bis vl4 (C-spline Curves durch korrespondierende Cps) harmonisch in Längsrichtung verlaufen.
Und zum anderen daran, dass die B-spline-Mcs „natürlich“ parametrisiert sind. Also die Parameterverteilung nicht durch ein Relabel- oder SubCurve-Objekt verändert ist. Dann sind die Kurvenpunkte ähnlich verteilt wie die Kontrollpunkte. Sind diese in Lofting-Richtung regelmäßig angeordnet, gilt dies auch für die Parameterkurven.
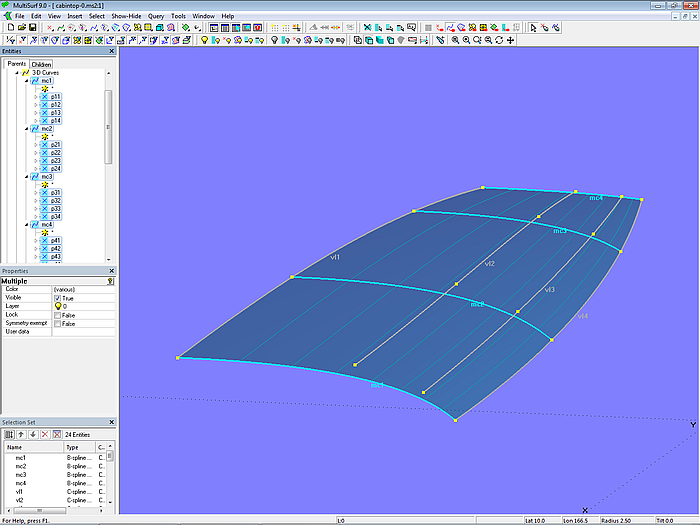
Modell cabintop-0.ms2 – C-spline Lofted Surface mit u-Parameterkurven und Vertexkurven
Bei einer Lofted Surface hängt die Form der Fläche vom Verlauf der erzeugenden Lofting Curves ab. Und diese wiederum entscheidend von der Parameterverteilung ihrer Mcs.
So viel vorab.
Nun zur Frage, ob sich der konkave Verlauf der Schnitte im Bereich der äußeren Ecke des Ausgangsmodell cabintop-0.ms2 beheben läßt, in dem man mit Relabel Einfluß auf die Parameterverteilung der Mcs nimmt, um den Verlauf der Lofting Curves zu kontrollieren.
Betrachten wir hierzu das Modell cabintop-e.ms2. Die vier B-spline Curves mc1, mc2, mc3 und mc4 sind nun die Basiskurven der eigentlichen Masterkurven der C-spline Lofted Surface cabintop, nämlich die SubCurves mc1_sub, mc2_sub, mc3_sub und mc4_sub. Jede ist mit jeweils 2 Beads sowie den System-Beads *0 und *1 definiert. An der vorderen SubCurve (mc4_sub) liegen die Beads ganz am Kurvenende ihrer Basiskurve mc4. Die Beads an den anderen Basiskurven sind so positioniert, das die Lofting Curves (angezeigt durch die u-Parameterkurven) ohne Schwingen auf die äußere Ecke zu laufen.
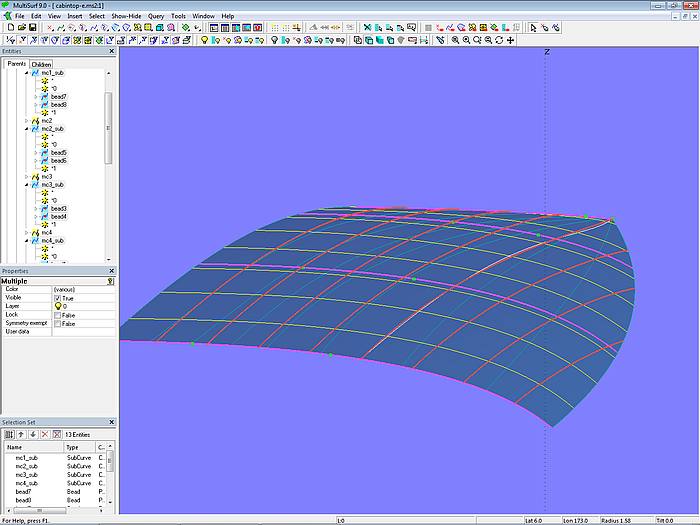
Modell cabintop-e.ms2 – Verlauf der u-Parameterkurven kontrolliert durch Relabel
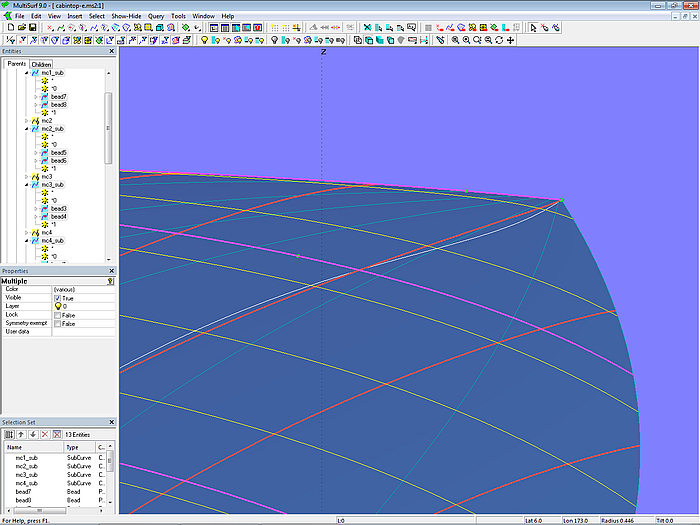
Modell cabintop-e.ms2 – Verlauf der u-Parameterkurven kontrolliert durch Relabel
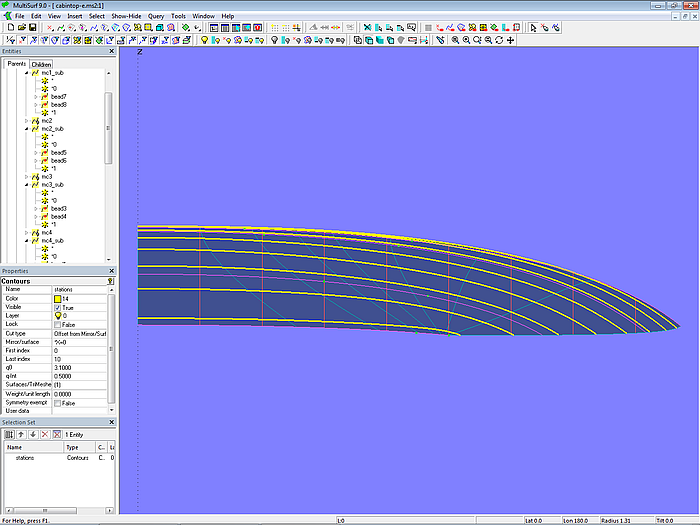
Modell cabintop-e.ms2 – Verlauf der u-Parameterkurven kontrolliert durch Relabel; der Spant hinter der Vorderkante des Aufbaudachs sieht unpassend aus.
Durch Relabeln der Basismasterkurven und den dadurch bewirkten Einfluß auf den Verlauf der Lofting Curves läßt sich der konkave Schnitt korrigieren. Aber stimmig sieht der Spant unmittelbar hinter der Vorderkante des Kajütdachs nicht aus. Seine Form paßt nicht zur Form von mc4. Es sieht erzwungen aus.
Weitere Lösungsansätze, wie
• Fläche in Längsrichtung in zwei Streifen teilen
• Mc4 erstreckt sich um die Ecke (mit PolyCurve oder B-spline Curve mit Dreifachpunkt)
• mehr Mcs mit mehr Cps
• B-spline Lofted Surface anstatt C-spline Lofted Surface
führen zu keinen besseren Ergebnissen.
1.7 Lösungsansatz F – runde Ecke
Was bleibt, ist, dass man eine Entwurfsbedingung aufgibt. Wie es aussieht, wenn mc4 doch eine Korbbogenform hat oder die Außenkante nach vorne etwas abfällt, wurde im Vorstehenden beschrieben. Die gravierenste Entwurfsforderung ist aber die nach der spitzen Ecke. Macht man eine Rundung wie in Modell cabintop-f.ms2, dann wird der Schnitt nicht mehr hohl. Die Vorderkante hat keine Korbbogenform und die Außenkante muß nicht abfallend verlaufen.
In Modell cabintop-f.ms2 ist die B-spline-Masterkurve mc4 mit zwei weiteren Cps (p45, p46) definiert. Da diese dicht bei Point p44 liegen, sind hier die Tickmarks enger beieinander als bei den anderen Mcs. Damit die u-Parameterkurven harmonisch zur runden Ecke laufen, werden die Mcs mc1, mc2 und mc3 über SubCurves relabeled. Alternativ könnte man auch diese Mcs mit je zwei weiteren Cps definieren. Das würde zwar den Aufwand etwas erhöhen, aber dann könnte die Vertexkurvenmethode angewendet werden, um auf anschauliche Weise einen strakenden Verlauf der u-Parameterkurven und damit der ganzen Fläche zu gewährleisten.
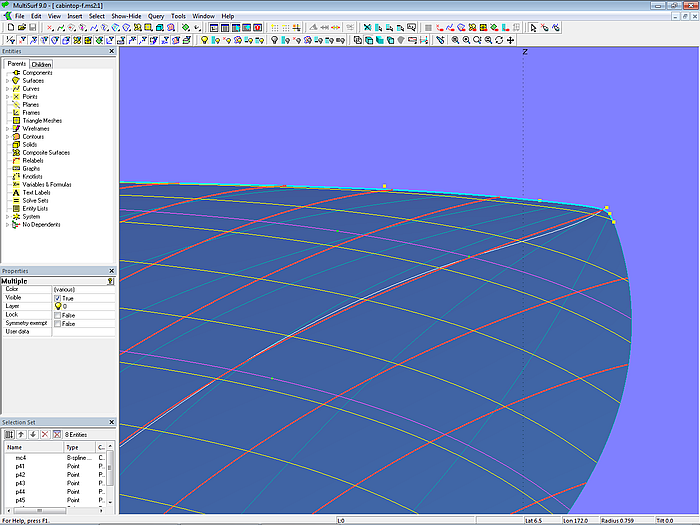
Modell cabintop-f.ms2 – Masterkurve mc4 definiert Vorderkante und Abrundung.
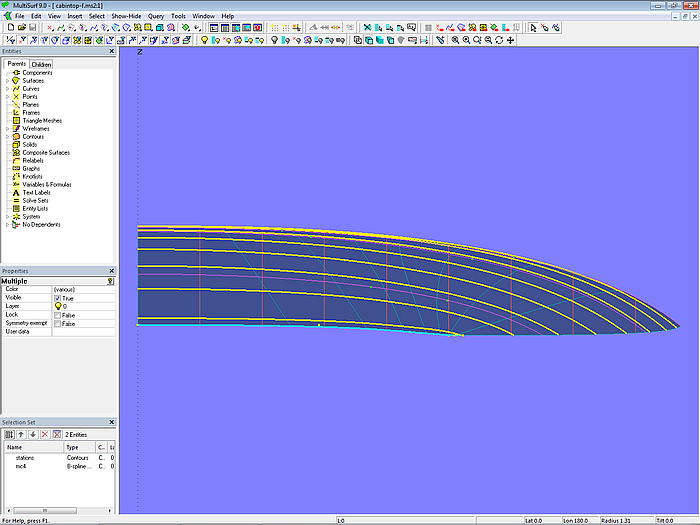
Modell cabintop-f.ms2 – Spantform bei abgerundeter Ecke
1.8 Lösungsansatz G – Tangent Boundary Surface
Bislang wurde versucht, die geforderte Form des Aufbaudachs durch eine C-spline Lofted Surface zu erzeugen. Diverse Ansätze wurden verfolgt, aber ohne Aufgabe von Vorgaben wurde kein zufriedenstellendes Ergebnis erreicht.
Liegt es an der falschen Flächenart? Die Vorgaben an die Geometrie aller vier Flächenkanten legt es nahe, statt einer C-spline Lofted Surface es mit einer Tangent Boundary Surface zu versuchen. Dies ist Modell cabintop-g.ms2. Curve1 ist die C-spline Curve vl1, Curve2 ist die B-spline Curve mc4, Curve3 die C-spline Curve vl4 und Curve4 die B-spline Curve mc1. Mit dem B-spline Graph graph1 wird mc1 stärker gewichtet als mc4.
Auch in diesem Modell ist der Schnitt durch die Ecke konkav.
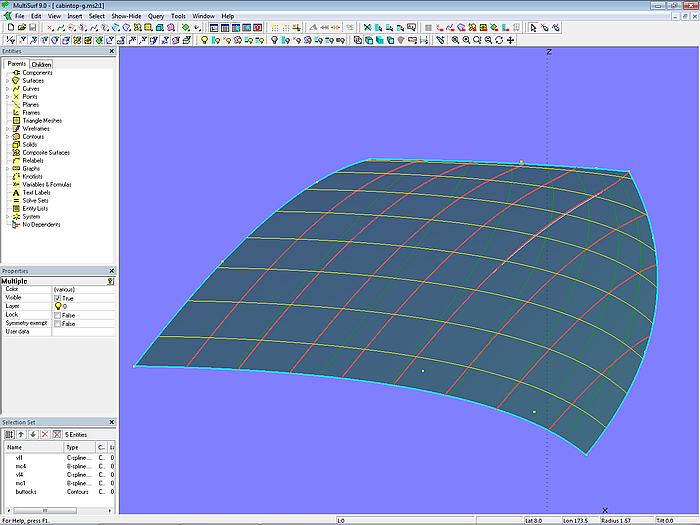
Modell cabintop-g.ms2 – Kajütdach als Tangent Boundary Surface
Control values
Das Innere der Tangent Boundary Surface kann über “Control values” (Anzahl in u- und v-Richtung wählbar) zusätzlich lokal geformt werden. Mit ihrer Hilfe kann der konkave Schnittverlauf minimiert werden.
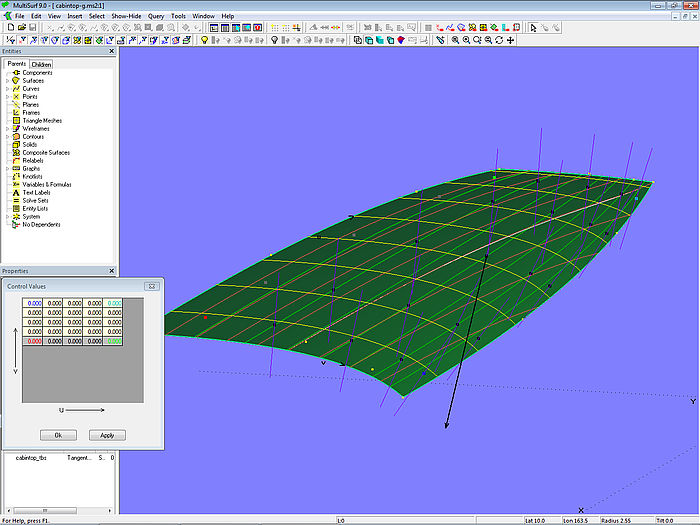
Modell cabintop-g.ms2 – das Innere der Tangent Boundary Surface kann mit “Control values” zusätzlich geformt werden.
Parameterverteilung
In Modell cabintop-g1.ms2 wird mc4 mit p44 als Vierfachpunkt definiert. Dadurch ändert sich ihre Parameterverteilung erheblich und die Lofting Curves (hier: v-Parameterkurven) verschieben sich in Richtung vordere äußere Ecke. Der Schnitt ist nahezu nicht mehr hohl, dafür sind die Spanten stark korbbogenförmig.
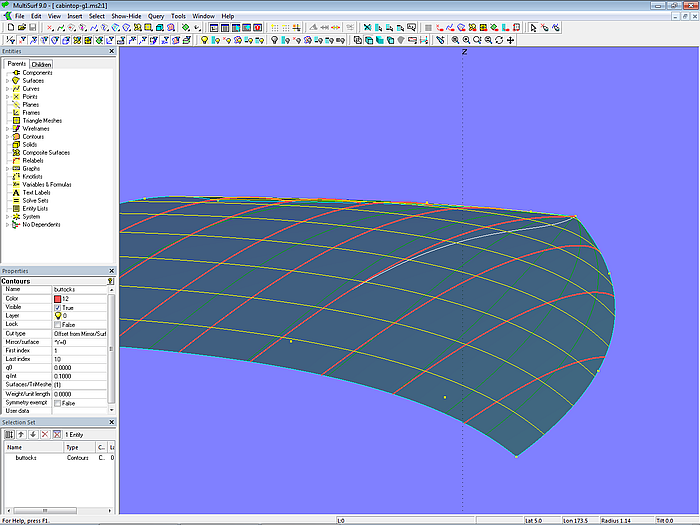
Modell cabintop-g1.ms2 – Tangent Boundary Surface mit p44 an mc4 als Vierfachpunkt
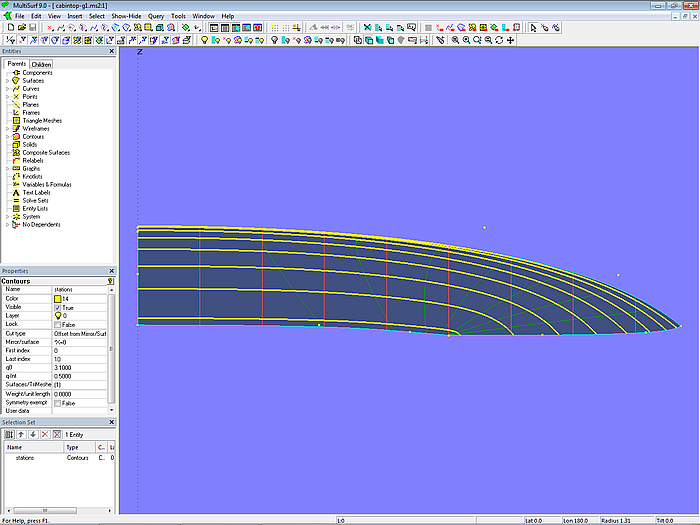
Modell cabintop-g1.ms2 – Spanten (p44 an mc4 als Vierfachpunkt)
2 Formeffekte bei Rümpfen
Dreht man das Aufbaudach hochkant und verformt etwas die Mcs, entsteht die Geometrie eines Bootsrumpfes. Auch beim Modellieren eines Rumpfes kann es vorkommen, dass Schnitte parallel zur Wasserlinie im Bereich des Übergangs zwischen Vorsteven und Bodenkontur konkav verlaufen.
Wie jeder andere Rumpfschnitt ist die Form der Wasserlinien das Resultat aus dem Verlauf der u-Parameterkurven der Rumpffläche. Wenn sie zum Vorsteven hin ansteigen, treten hohle Wasserlinien auf. Ein Rumpf mit engem Vorfuß ist dafür besonders anfällig.
In Tutorium 1, Modellieren von Rundspantrümpfen, wird im Zusammenhang mit der Vertexkurvenmethode für strakende Rumpfflächen mit C-spline Lofted Surfaces berichtet, wie sich hohle Wasserlinien vermeiden lassen. Diese sind kein Naturgesetz beim rechnergestützten Rumpfsentwurf.
Falls hohle Wasserlinien im Bugbereich kein Entwurfsmerkmal sein sollen, kann nach dem gleichen Ansatz Abhilfe geschaffen werden, der auch am Aufbaudach angewendet wurde: man kontrolliert den Verlauf der Lofting Curves. Dafür wird die Parametrisierung der Mcs beeinflußt – entweder durch Anordnung der Cps oder mit Hilfe der Objekte SubCurve und Relabel.
Wenn Wasserlinien nicht absichtlich hohl verlaufen sollen, muß der Anstieg der u-Parameterkurven hin zum Steven vermindert werden. Dazu verschiebt man die unteren Cps der Bug-Mc etwas nach hinten. So steigen die u-Parameterkurven weniger steil an und die Wasserlinien werden gerade.
2.1 Rumpf mit eckigem Vorfuß
Betrachten wir als Beispiel das Modell hull-0.ms2. Der Rumpf ist eine C-spline Lofted Surface mit 4 B-spline-Masterkurven (Mcs). Jede ist definiert mit 5 Kontrollpunkten (Cps). Der Vorsteven mc1 soll vertikal verlaufen, mit spitzer Ecke am Ende.
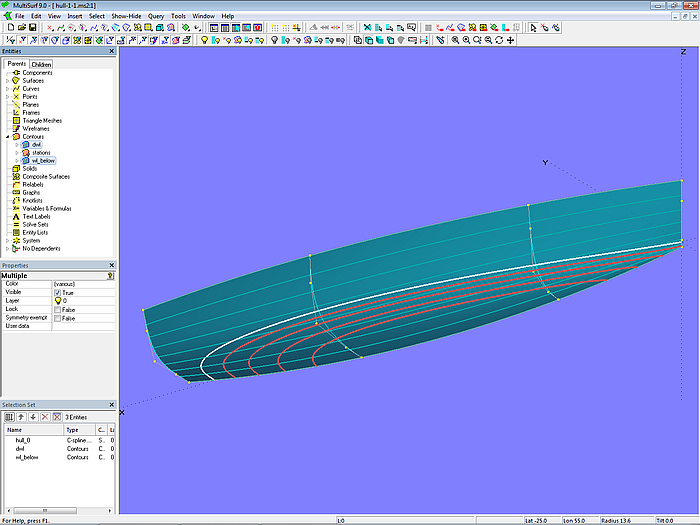
Modell hull-0.ms2 – Bootsrumpf als C-spline Lofted Surface mit 4 B-spline Masterkurven
Die Wasserlinien im unteren Bugbereich sind hohl.
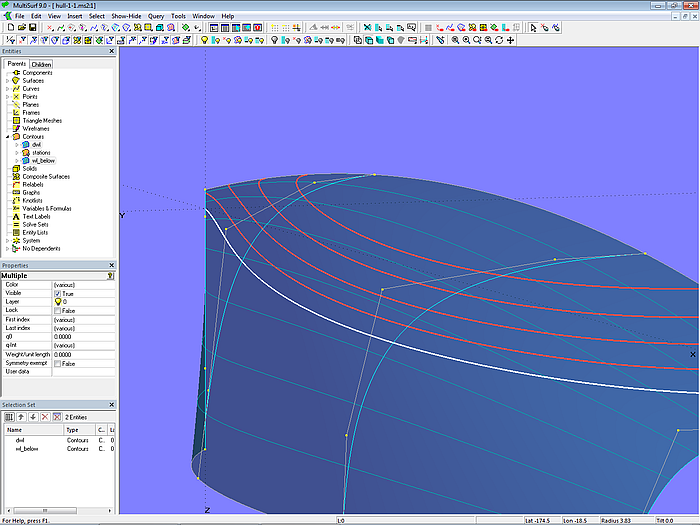
Modell hull-0.ms2 – hohle Wasserlinien im unteren Vorstevenbereich
Was ist zu tun? Die Parameterkurven müssen zum Fuß des Vorstevens hin laufen. Das heißt, die Parameterverteilung an der Bug-Mc muß so geändert werden, dass sich die Tickmarks in diesem Bereich konzentrieren. Dies kann auf zwei Weisen geschehen:
• Konzentration der Cps, Mehrfach-Cp
• Relabel mit SubCurve (oder Relabel-Objekt)
Im Modell hull-1.ms2 ist die erste Variante gewählt. An der Bug-Mc (mc1) liegt p13 dicht über p14, der zweifach in der Definition gewählt ist.
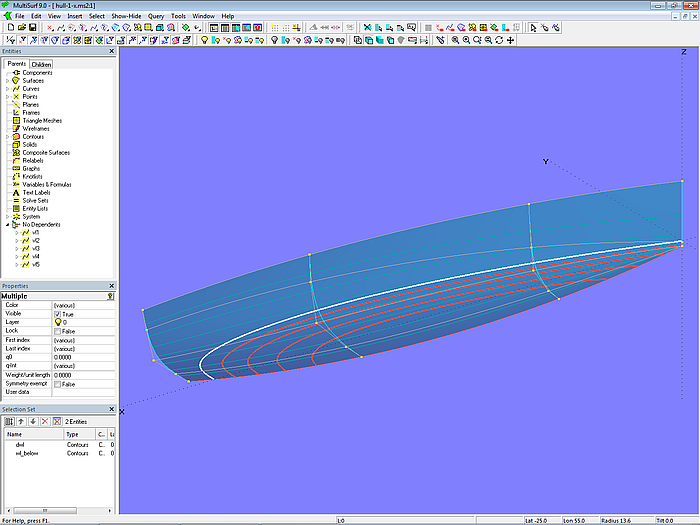
Modell hull-1.ms2 – Konzentration der Parameterkurven im Vorfußbereich; p13 liegt nahe bei Doppelpunkt p14.
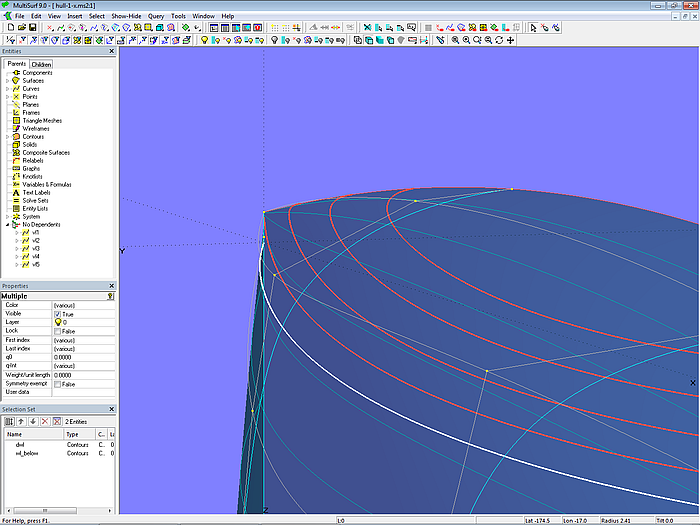
Modell hull-1.ms2 – die Parameterkurven laufen zum unteren Vorfußbereich; p14 ist Doppelpunkt.
2.2 Rumpf mit rundem Vorfuß
Weniger ausgeprägt ist der hohle Verlauf der Wasserlinien im Bereich des Vorstevenfußes, wenn der Übergang zur Bodenkontur abgerundet ist. Hohle Wasserlinien werden auch hier auf die gleiche Weise beseitigt, nämlich in dem man Einfluß nimmt auf den Verlauf der Lofting Curves. Diese müssen zum Vorfuß hin laufen, am besten etwas von oben herab. Dann entstehen keine hohlen Wasserlinien. Am einfachsten läßt sich der Verlauf beeinflussen durch die Anordnung der Cps. Dort, wo sie dicht beieinander liegen, laufen auch die Lofting Curves hin.
Ein Beispiel zeigt Modell hull-2.ms2. Damit sich die Lofting Curves im Vorfuß konzentrieren, ist Point p13 zweifach enthalten in der Liste der Cps für mc1.
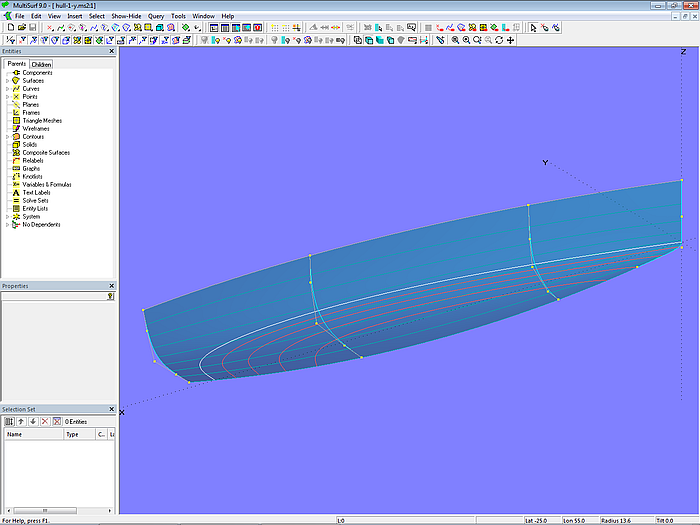
Modell hull-2.ms2 – Konzentration der Parameterkurven im Vorfußbereich; p13 ist Doppelpunkt.
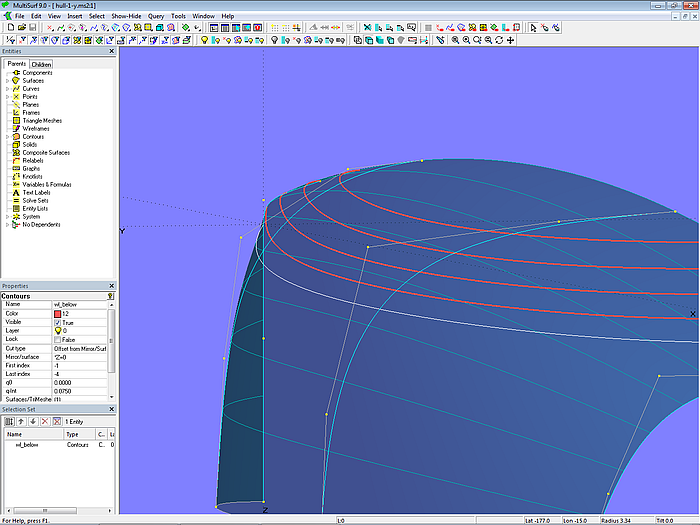
Modell hull-2.ms2 – Konzentration der Parameterkurven im Vorfußbereich; p13 ist Doppelpunkt.
3 Formeffekte bei Foil Lofted Surface und Arc Lofted Surface
In Tutorium 6, Modeling a Rudder in MultiSurf, wird über Methoden und Strategien beim Modellieren von Rudern berichtet. Ein Abschnitt befaßt sich mit Formeffekten bei Foil Lofted Surfaces, die durch unterschiedliche Parametrisierung der Masterkurven verursacht werden. Es werden mehrere Methoden vorgestellt, um den Verlauf der Lofting Curves zu kontrollieren.
In Modell rudder_floft.ms2 sind die 3 in Spannweitenrichtung verlaufenden Mcs alle B-spline Curves mit gleichem Degree und gleicher Anzahl der Cps. Korrespondierende Cps haben außerdem die gleiche Z-Position. Es ergibt sich somit eine identische Parameterverteilung und infolgedessen ein regelmäßiger horizontaler Verlauf der Lofting Curves (Foil Curves).
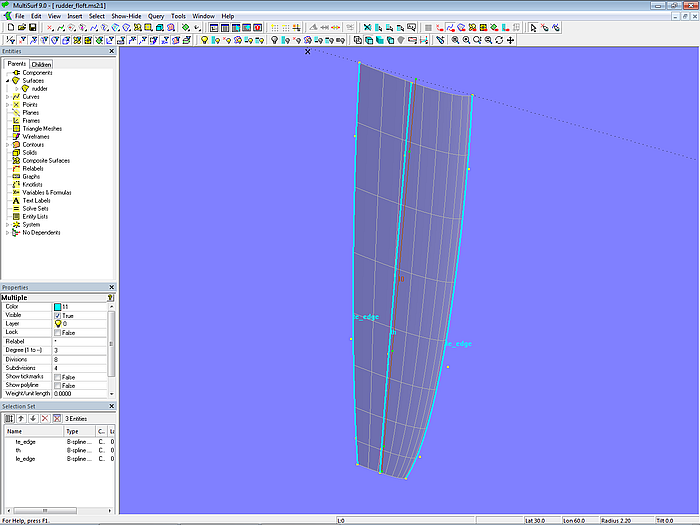
Modell rudder_floft.ms2 – Ruderfläche als Foil Lofted Surface; gleiche Kurvenart und Anzahl der Cps bei gleicher Z-Position ergibt gleiche Parameterisierung der Masterkurven und einen regelmäßigen Verlauf der Parameterkurven.
In Tutorium 13, Decks und Aufbauten, wird an einem Beispiel erklärt, wie sich ein Deck mit einer Arc Lofted Surface erzeugen läßt. Bei der Konstruktion dieses Modells wird explizit auf gleiche Parametrisierung der Masterkurven geachtet. In Modell deck_arcloft.ms2 ist Mc1 die Oberkante des Rumpfes (C-spline Lofted Surface), Mc2 eine dazu relative C-spline Curve mit gleicher Anzahl und Längsposition der Cps und Mc3 (Projected Curve) ist die Projektion von Mc2 auf die Mittschiffsebene. Somit ist eine identische Parameterverteilung der Mcs im Modell festverdrahtet und die Lofting Curves (Arcs) laufen alle in Spantebene. Was nicht der Fall wäre bei ungleicher Parametrisierung der Mcs.
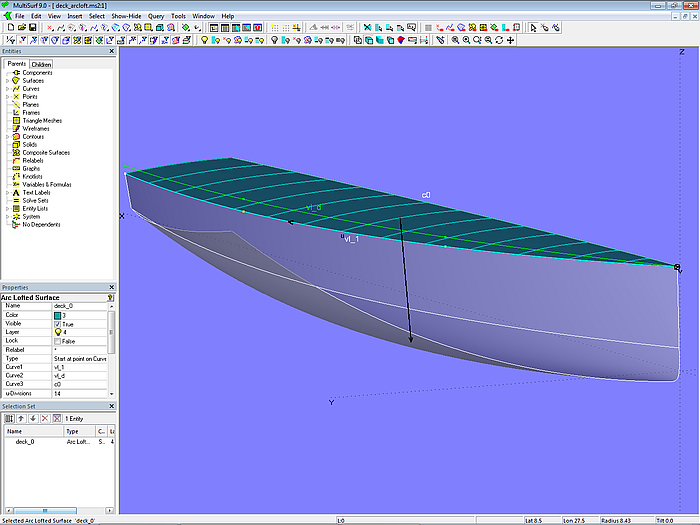
Modell deck_arcloft.ms2 – Deck als Arc Lofted Surface; aufgrund der identischen Parametrisierung der Mcs verlaufen die Lofting Curves (Arcs) in Spantebene.
So viel zu Formeffekten bei Lofted Surfaces.
======================================================================================