Über Rumpfformen mit auslaufendem Knick
Zwei Lösungsansätze
von Reinhard Siegel
März 2024
Inhalt
Einleitung
1 Rumpf mit Teilknick – der Zwei-Flächen-Ansatz
1.1 Masterkurven tangential verbunden
1.2 Masterkurven aufteilen in SubCurves
2 Rumpf mit Teilknick – der Eine-Fläche-Ansatz
3 Beispiele
3.1 Segelschiffsrumpf – rundes Heck mit auslaufendem Knick
3.2 Motorbootrumpf – auslaufender Knick im Vorschiff
4 Zusammenfassung
5 Anhang – die Vertexkurven-Methode
Einleitung
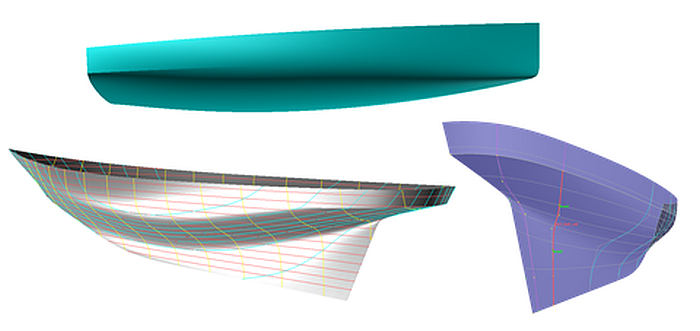
Die Form von Schiffs- und Bootsrümpfen ist vielfältig. Dabei verändern Spanten, also Querschnitte durch die Rumpffläche, harmonisch ihre Form von Bug bis Heck. Ihrerseits können Spanten selbst durchaus einen unstetigen Verlauf in ihrer Form aufweisen. Sollen beispielsweise bei einem Motorbootsrumpf die Spanten im Vorschiffsbereich stark ausfallen, kann mit einem Knick im Spantverlauf verhindert werden, dass das Deck übermäßig breit wird. Gleiches gilt für Segelbootsrümpfe, hier im Heckbereich. Verbindet man diese Knickpunkte der Spanten, so entsteht eine in Längsrichtung des Rumpfes verlaufende Knickkurve. Je nach Bootstyp kann die Knickkurve relativ nah am oberen Rand des Rumpfes verlaufen oder im Spantgurtmaß deutlich tiefer liegen.
Eine Knickkurve kann sich von Bug bis Heck über die gesamte Rumpflänge erstrecken. Dann ändert sich in Längsrichtung allmählich die unterschiedliche Richtung in der Spantkurve in der Umgebung ihres Knickpunktes, verschwindet aber nicht ganz.
Eine Knickkurve kann aber auch nur in einem bestimmten Rumpfbereich auftreten. Dann verschwindet allmählich die Unstetigkeitsstelle in der Spantkurve und die Spanten verlaufen glatt.
Einen Rumpf mit durchgehendem Knick zu modellieren ist einfacher als einen Rumpf mit Teilknick. In Tutorium 2, Rundspantrumpf mit durchlaufendem Knick, wird erstere Konstruktionsausgabe behandelt. In Tutorium 3, Rundspantrumpf mit auslaufendem Knick, wird ein Verfahren vorgestellt, wie ein Rumpf mit einem Teilknick im Heck erzeugt werden kann (in Tutorium 22, Drei Konstruktionsaufgaben, wird die gezeigte Methode für einem Katamaranrumpf angewendet).
Im vorliegenden Tutorium werden weitere Verfahren erörtert, wie man unterschiedliche Rumpfformen mit einem Teilknick modellieren kann.
Verwendete Abkürzungen:
Cp: Kontrollpunkt, Stützpunkt (control point, support point); synonym verwendet
Mc: Masterkurve, Stützkurve (master curve, support curve); synonym verwendet
cp1, cp2, ...: bezeichnet den 1., 2. ... Punkt in der Liste der Kontrollpunkte einer Kurve. Es ist kein Objektname.
mc1, mc2, ...: bezeichnet die 1., 2. ... Kurve in der Liste der Stützkurven einer Fläche. Es ist kein Objektname.
Im Folgenden werden die MultiSurf-Namen für Punkt-, Kurven- und Flächenarten verwendet. Das ergibt zwar „denglische“ Sätze, soll aber dem Verständnis und der Nachvollziehbarkeit dienen.
1 Rumpf mit Teilknick – der Zwei-Flächen-Ansatz
Beim Zwei-Flächen-Ansatz wird die Knickkurve verlängert, so dass sie sich über die gesamte Rumpflänge erstreckt. Sie verläuft also auch in einem Bereich, in dem die Spanten keinen Knickpunkt haben, sondern glatt verlaufen.
Entlang der Knickkurve wird der Rumpf in eine obere Fläche und eine untere Fläche aufgeteilt. Um diese beiden Flächen zu erzeugen, gibt zwei Möglichkeiten:
- Masterkurven tangential verbinden
- Masterkurven aufteilen in SubCurves
1.1 Masterkurven tangential verbinden
Da diese Methode bereits in Tutorium 3 beschrieben wird, soll das wesentliche Vorgehen am Beispiel des Modells sailboat-tangent_mcs.ms2 kurz zusammengefaßt werden. Beide Flächen sind C-spline Lofted Surfaces (topside, bottom), die von der gleichen Anzahl Masterkurven (Mcs) gestützt werden. Alle Mcs sind B-spline Curves mit gleichem Grad („Degree“). Die Mcs für eine Fläche haben die gleiche Anzahl Kontrollpunkte (Cps). Der letzte Cp einer Seiten-Masterkurve ist gleichzeitig der erste Cp der korrespondierenden Boden-Mc. Die Mcs für Seite und Boden sind also separate B-spline-Kurven, berühren sich aber.
Im hinteren Bereich des Rumpfes, wo die Spanten einen Knickpunkt aufweisen sollen, stoßen die Mc-Paare von Seite und Boden mit unterschiedlicher Tangentenrichtung aneinander. Im vorderen Rumpfbereich, wo die Spanten glatt verlaufen sollen, berühren sich die Mcs tangential.
Anders als in Tutorial 3 wird in Modell sailboat-tangent_mcs.ms2 für die tangentiale Verbindung das Objekt Tangent Point verwendet. Dazu ist auf jeder der vorderen Mcs für die Fläche bottom ein Bead am Kurvenanfang (t = 0) angeordnet, von dem ein Tangent Point abhängt. Mit Cp1 und diesen beiden Punkten sind jeweils die Mcs von topside definiert. Durch den Tangent Point ist der tangentiale Anschluß der Mcs der oberen und unteren Fläche festverdrahtet.
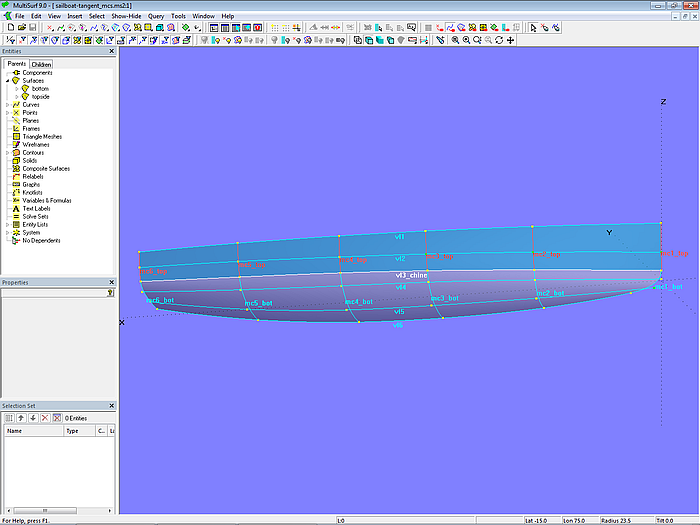
Modell sailboat-tangent_mcs.ms2 – je 6 Mcs stützen die C-spline Lofted Surfaces topside und bottom. Im Bereich ohne Knick stoßen die Mcs für Seite und Boden tangential aneinander. Vertexkurven verbinden korrespondierende Kontrollpunkte.
Vorteil:
Bei dieser Konstruktion des Modells läßt sich die Vertexkurven-Methode zum Straken verwenden (siehe Anhang). Die Knickkurve ist gleichzeitig eine Vertexkurve (C-spline Curve vl3_chine). Ihr Verlauf wird durch die entsprechenden Cps direkt bestimmt.
Nachteil:
Im glatten Rumpfbereich (ohne Knick in den Spanten) stoßen die Mcs für Seite und Boden im Verbindungspunkt zwar mit gleicher Tangentenrichtung aneinander, aber die Krümmung kann unstetig sein. Zur Kontrolle des Krümmungsverlaufs kann man ein korrespondierendes Mc-Paar zu einer PolyCurve zusammensetzen und sich deren Curvature Profile über View/ Display/ Profile/ Curvature (oder Toolbar-Schaltfläche) anzeigen lassen.
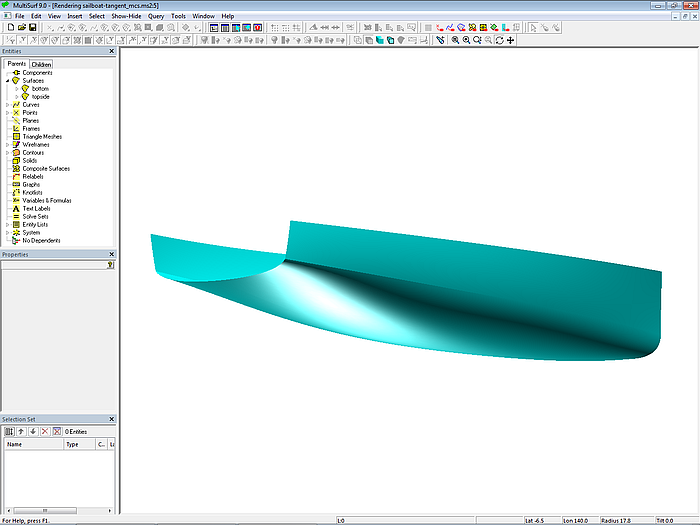
Modell sailboat-tangent_mcs.ms2 – auslaufender Knick im Heck
1.2 Masterkurven aufteilen in SubCurves
Wäre es nicht auch möglich, im Bereich ohne Knick von Rumpfoberkante bis zur Bodenkontur durchgehende Mcs zu verwenden, diese aber dann in je 2 SubCurves zu teilen? Dann stoßen die Mcs für Seite und Boden im Verbindungspunkt sowohl mit gleicher Tangentenrichtung als auch gleicher Krümmung aneinander In Modell sailboat-subcurve_mcs-0.ms2 wird dies ausprobiert.
Basisrumpf
Ein Rumpf mit Teilknick ist nicht allzu weit von einem glatten Rumpf entfernt. Der Bereich ohne Knick ist größer als der Bereich mit Knick. Darum liegt es nahe, zunächst als Ausgangspunkt einen glatten Rumpf zu modellieren, der bis auf den auslaufenden Knick die gewünschte Form aufweist. Dabei kann die Vertexkurven-Methode angewendet werden, so dass korrespondierende Cps harmonisch in Längsrichtung des Rumpfes ihre Position ändern und dadurch auch die u-Parameterkurven straken. Die Mcs haben dann untereinander eine ähnliche Parameterverteilung, die sie auf Teilkurven (SubCurves) vererben. Näheres zur Vertexkurven-Methode siehe Anhang.
Basisfläche ist die C-spline Lofted Surface hull_fair, definiert mit 6 B-spline-Mcs und jeweils 6 Cps. Zum Straken von hull_fair wird die Vertexkurven-Methode mit den C-spline Curves vl1 bis vl6 verwendet.
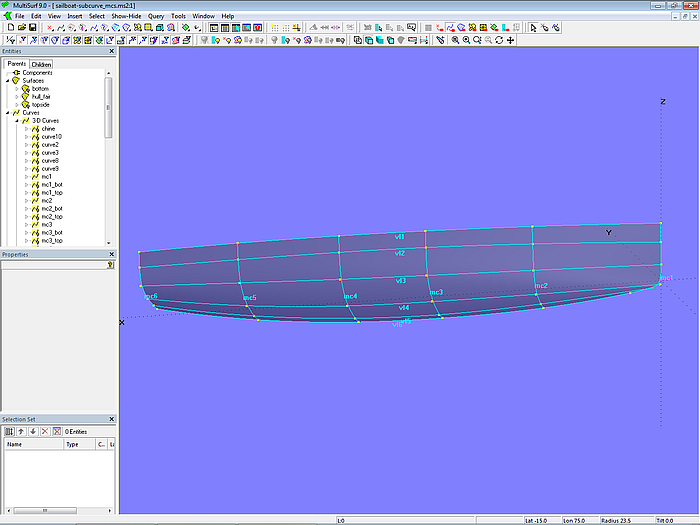
Modell sailboat-subcurve_mcs-0.ms2 – die C-spline Lofted Surface hull_fair ohne Knick wird von 6 Mcs gestützt. Korrespondierende Kontrollpunkte sind durch Vertexkurven als Strakhilfe verbunden.
Straken die Vertexkurven, straken auch die u-Parameterkurven (Lofting Curves) und damit die Fläche.

Modell sailboat-subcurve_mcs-0.ms2 – Vertexkurven und u-Parameterkurven (Lofting Curves) der C-spline Lofted Surface hull_fair
Vordere Masterkurven teilen
Die vorderen Mcs dieser Basisfläche werden nun geteilt, um die Mcs für die Seiten- und Bodenfläche im Rumpfbereich ohne Knick zu erzeugen. Je ein Bead (e1 bis e4) wird auf die 4 vorderen Mcs (mc1 bis mc4) gesetzt und mit diesen die SubCurves mc1_top, mc1_bot, mc2_top, mc2_bot etc. bestimmt. Mit den Beads und den beiden freien Punkten p53_a und p63_a an der X-Position von mc5 und mc6 wird dann die Knickkurve chine als C-spline Curve definiert. Im Gegensatz zu Modell sailboat-tangent_mcs.ms2 entspricht die Knickkurve chine nicht mehr der Vertexkurve vl3.
Die hinteren Mcs im Knickbereich (mc5_top, mc5_bot sowie mc6_top und mc6_bot), die den Rumpf nach außen und unten „ausbeulen“, werden aus dem Modell sailboat-tangent_mcs.ms2 übernommen.
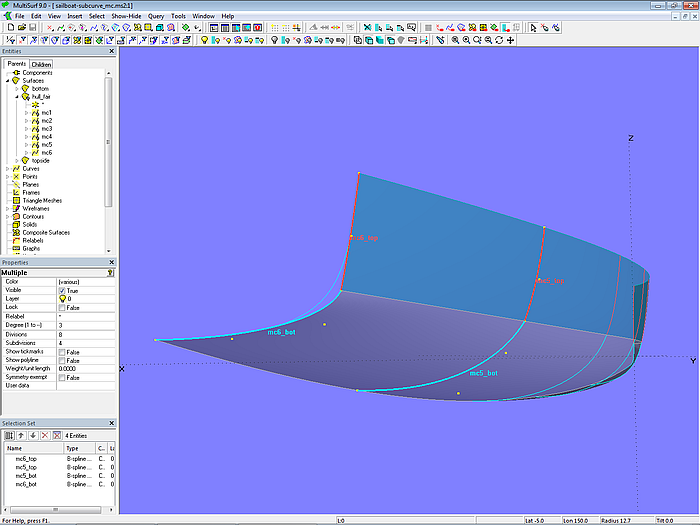
Modell sailboat-subcurve_mcs-0.ms2 – die Flächen topside und bottom werden im Heckbereich von den B-spline-Mcs mc5_top, mc5_bot, mc6_top sowie mc6_bot gestützt; sie stoßen mit einem Knick aneinander.
Nach dieser Vorarbeit können nun analog zu Modell sailboat-tangent_mcs.ms2 abschließend die C-spline Lofted Surfaces topside und bottom erzeugt werden.
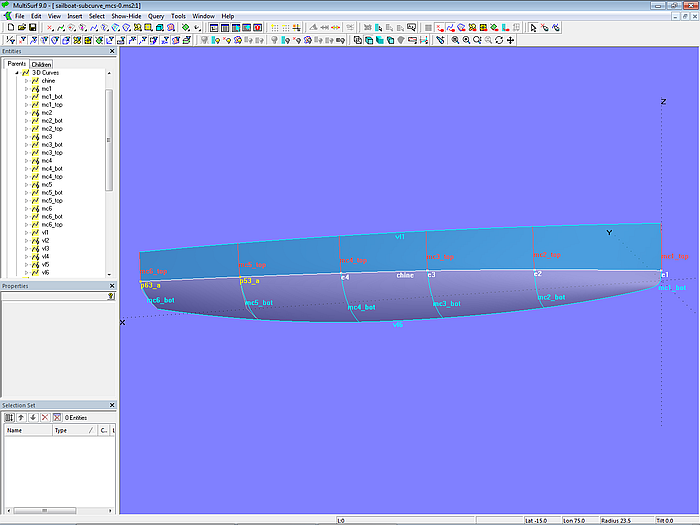
Modell sailboat-subcurve_mcs-0.ms2 – Masterkurven der C-spline Lofted Surfaces topside und bottom. Knickkurve ist chine.
Verlauf der u-Parameterkurven
Betrachten wir für den Strak der beiden Flächen topside und bottom den Verlauf ihrer u-Parameterkurven. Es ist ersichtlich, dass sie für bottom nicht harmonisch verlaufen. Der Grund dafür ist der Unterschied in der Parameterverteilung der hinteren Mcs (B-spline Curves) zur Parameterverteilung der vorderen Mcs (SubCurves). Die Parameterverteilung der vorderen Mcs ist ähnlich, da sie von den durchgehenden Mcs von hull_fair auf die SubCurves vererbt wird.

Modell sailboat-subcurve_mcs-0.ms2 – u-Parameterkurven (Lofting Curves) der C-spline Lofted Surfaces topside und bottom. Durch die unterschiedliche Parameterverteilung der Mcs im Heckbereich verlaufen die u-Parameterkurven nicht regelmäßig.
In der Praxis wird man beim Bau eines solchen Rumpfes die Planken oder Leisten entlang der hinteren Mallen etwas verschieben, bis sie regelmäßig verlaufen.
Möglichkeit 1: hintere Mcs mit SubCurve relabeln
Übertragen auf unser Modell heißt das, dass den Kurvenpunkten der beiden B-spline Curves mc5_bot und mc6_bot andere t-Parameterwerte zugewiesen werden müssen (Re-Parametrisierung, Relabel). Die Kurvenform ändert sich nicht beim Relabeln, auch die Position der Kurvenpunkte bleibt gleich, lediglich der zugehörige t-Parameterwert wird verändert. Am einfachsten, weil sehr anschaulich, kann man eine Kurve mit dem Objekt SubCurve relabeln.
Da wir von der Fläche hull_fair wissen, dass ihre Mcs eine regelmäßige Anordnung ihrer Cps in Längsrichtung haben, und folglich auch eine regelmäßige Parameterverteilung, ist es naheliegend, diese Mcs nicht zu ändern, sondern nur die hinteren Mcs zu relabeln. Dies wird in Modell sailboat-subcurve_mcs-1.ms2 demonstriert.
Zunächst wird der Bead bead1 auf mc5_bot gesetzt, sowie der Bead bead2 auf mc6_bot. Dann wird mit den Control Beads {*0 bead1 *1} die SubCurve mc5_bot_sub erzeugt, sowie mit {*0 bead2 *1} die SubCurve mc6_bot_sub. Schließlich werden bei der Definition der Bodenfläche bottom diese beiden SubCurves anstelle von mc5_bot und mc6_bot eingesetzt.
Verschiebt man nun die Beads bead1 und bead2, verschieben sich auch die u-Parameterkurven. Verlaufen diese aus verschiedenen Ansichten betrachtet harmonisch, strakt die Fläche.
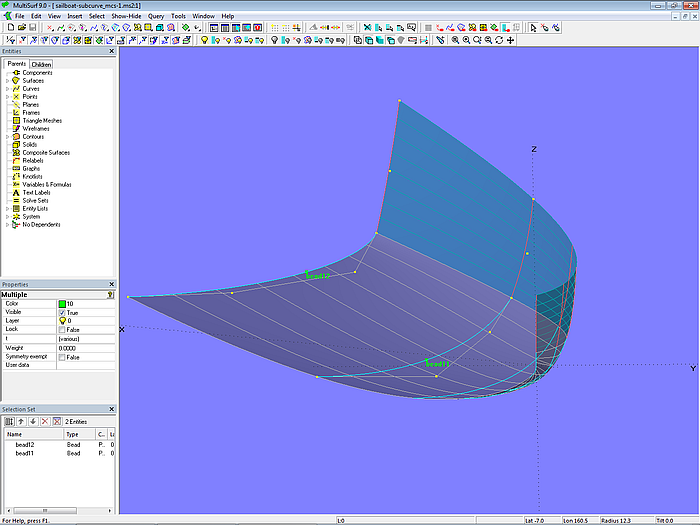
Modell sailboat-subcurve_mcs-1.ms2 – mc5_bot und mc6_bot mit SubCurves relabeled. Durch Verschieben der Beads bead1 und bead2 wird der Verlauf der u-Parameterkurven beeinflußt.
Modell sailboat-subcurve_mcs-1.ms2
Möglichkeit 2: hintere Mcs mit zusätzlichem Kontrollpunkt
Statt die hinteren Mcs mc5_bot und mc6_bot mit Hilfe von SubCurves zu relabeln, kann man alternativ diese beiden B-spline Curves mit je einem zusätzlichen Kontrollpunkt definieren. Auf diese Weise gewinnt man etwas mehr Freiraum – man kann diesen Kurven die gewünschte Form geben und dabei gleichzeitig den Verlauf der Lofting Curves beeinflussen.
Dieses Vorgehen wird in Modell sailboat-subcurve_mcs-2.ms2 gezeigt. Mc5_bot und mc6_bot haben nun 5 Cps statt 4 Cps. Ihre inneren Cps sind so positioniert, dass die Kurven die gleiche Form haben wie die Mcs in den bereits vorgestellten Modellen, aber gleichzeitig ein regelmäßiger Verlauf der u-Parameterkurven resultiert.
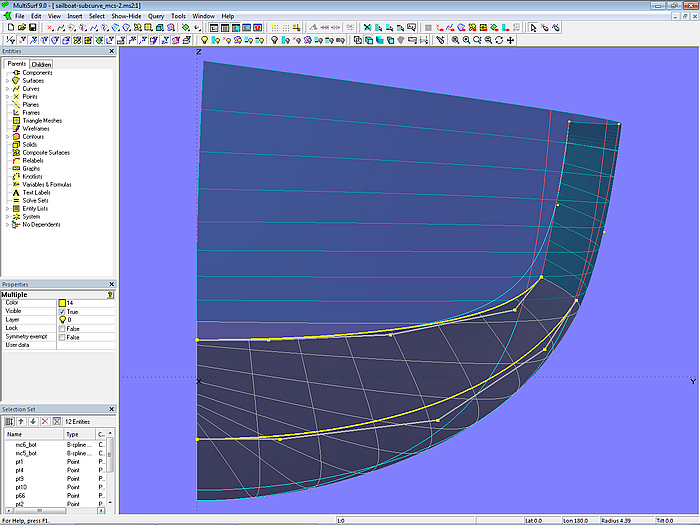
Modell sailboat-subcurve_mcs-2.ms2 – B-spline Curves mc5_bot und mc6_bot definiert mit zusätzlichem Kontrollpunkt
Vorteil:
Für den glatten Basisrumpf (hull_fair) kann die Vertexkurven-Methode angewendet werden. Die Mcs im Bereich des Rumpfes ohne Spantknick werden als Ganzes geformt, nicht getrennt. Sie sind richtungs- und krümmungsstetig. Die Parameterverteilung der Mcs ist ähnlich. Der Knickverlauf (chine) läßt sich ändern, ohne dass gleichzeitig die Form der Masterkurven geändert werden muß.
Nachteil:
Der Aufwand ist etwas größer als beim Ansatz mit separaten Mcs (Modell sailboat-tangent_mcs.ms2), da man erst einen strakenden Basisrumpf modellieren muß. Zwar kann die Vertexkurven-Methode für hull_fair angewendet werden, auch kann der Knickverlauf mit Hilfe der C-spline Curve chine gestrakt werden. Da es aber keine korrespondieren Cps an den vorderen Mcs gibt, lassen sich solche Strakhilfskurven für die Positionierung der inneren Cps der hinteren B-spline-Mcs (mc5_top, mc5_bot, mc6_top, mc6_bot) nicht erzeugen. Darum muß man bei der Anordnung der Cps für diese Mcs neben der gewünschten Form auch den harmonischen Verlauf der u-Parameterkurven (Lofting Curves) der C-spline Lofted Surfaces topside und bottom im Blick haben. Durch Relabeln mit SubCurve oder mit zusätzlichen Cps muß man die Parameterverteilung der Mcs im Knickbereich beeinflußen.
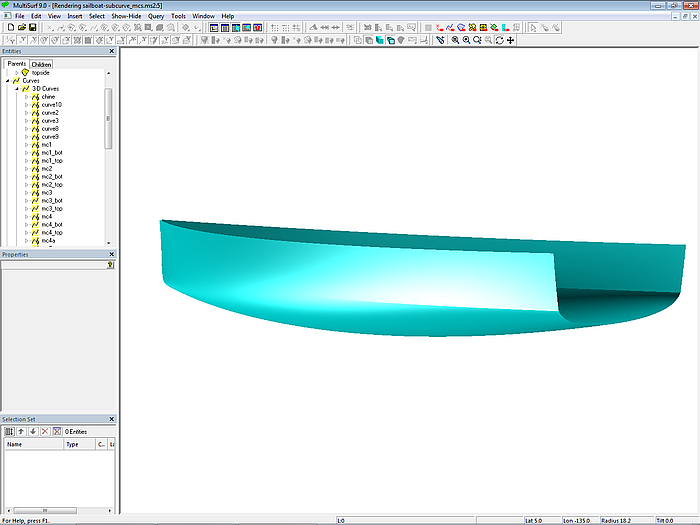
Modell sailboat-subcurve_mcs-2.ms2
2 Rumpf mit Teilknick – der Eine-Fläche-Ansatz
Bei den bislang vorgestellten Modellen sailboat-tangent_mcs.ms2 und sailboat-subcurve_mcs.ms2 wird der Rumpf entlang der Knickkurve in zwei Flächen aufgeteilt: eine Seitenfläche und eine Bodenfläche werden von separaten Mcs gestützt. Beim Eine-Fläche-Ansatz werden ausschließlich Mcs verwendet, die von Oberkante bis Unterkante Rumpf durchlaufen. Für die hinteren Mcs, die einen Knick aufweisen, kommen PolyCurves zum Einsatz. Mit dieser Kurvenart werden die Kurvensegmente für Rumpfseite und Rumpfboden zu einer Kurve zusammengefaßt.
Ausgehend vom Modell sailboat-subcurve_mcs-0.ms2 wird der Eine-Fläche-Ansatz in Modell sailboat-polycurve_mcs-0.ms2 gezeigt. Die SubCurves (mc1_top, mc1_bot etc.) an den vorderen Mcs sind nicht mehr erforderlich. Die B-spline Curves mc5_top und mc5_bot sowie mc6_top und mc6_bot sind zu den PolyCurves mc5_poly und mc6_poly zusammengefügt.
Eine Anmerkung zum Objekt PolyCurve – es gibt zwei Varianten der PolyCurve, bestimmt über den Eintrag „Yes/No“ in der Zeile „Specify end t-values“ im Properties Manager. Die Voreinstellung ist „No“. Die Kurve wird dann so erzeugt, dass die Kurvenpunkte gleichmäßig über der Länge verteilt sind. Soll der jeweilige t-Parameterwert am Ende der einzelnen PolyCurve-Segmente vorgegeben werden, muß „Yes“ ausgewählt werden.
Wir setzen „Specify end t-values“ auf „Yes“ und geben beiden PolyCurve-Mcs probehalber den Wert 0.220 für das Ende der Segmente mc5_top und mc6_top.
Die finale Fläche mit Teilknick kann nun mit den B-spline-Mcs mc1 bis mc4 sowie den beiden PolyCurves mc5_poly und mc6_poly erzeugt werden (C-spline Lofted Surface hull_w_chine).
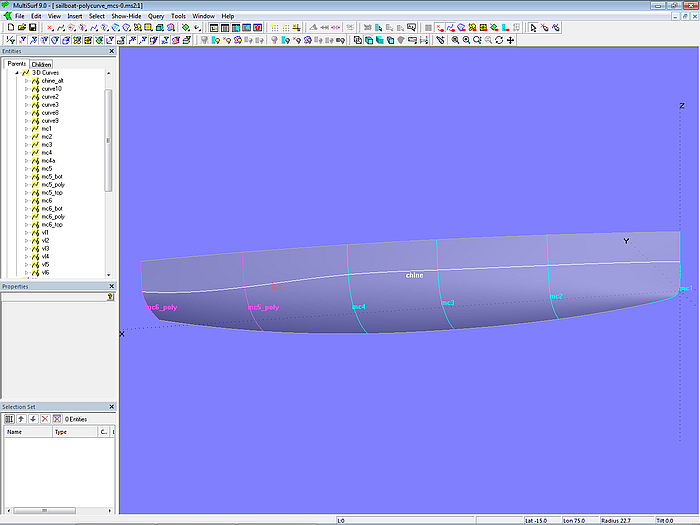
Modell sailboat-polycurve_mc-0s.ms2 – C-spline Lofted Surface hull_w_chine mit durchgehenden B-spline-Mcs vorne und PolyCurves im Heckbereich. End t-value der PolyCurve-Mcs probehalber gesetzt auf 0.220.
Beim Zwei-Flächen-Ansatz ist chine gleichbedeutend der EdgeSnake entlang der Unterkante der Fläche topside bzw. entlang der Oberkante der Fläche bottom. Dagegen ist beim Eine-Fläche-Ansatz chine eine UVSnake in u-Richtung, definiert mit einem Magnet, dessen u-Wert gleich dem end t-value der PolyCurve-Mcs ist. Chine ist also eine ganz bestimmte u-Parameterkurve.
Um die UVSnake chine für die Fläche hull_w_chine zu erzeugen, setzen wir den Magnet m_chine auf die Fläche und wählen für seinen u-Wert den end t-value, der auch für die PolyCurves mc5_poly und mc6_poly eingesetzt ist.
Der end t-value für mc5_poly und mc6_poly muß passend gewählt werden, damit die UVSnake chine strakt. Bei dem probehalber verwendeten Wert von 0.220 verläuft chine nicht harmonisch. Der Kurvenpunkt an den vorderen Mcs, der zu diesem t-Parameterwert gehört, liegt näher in Richtung Kurvenanfang als bei den hinteren Mcs.
Da an den vorderen Mcs nichts geändert werden sollte – die u-Parameterkurven der Basisfläche hull_fair straken – muß man sich an den passenden Wert herantasten. Bei einem end t-value von 0.296 für die PolyCurves (Magnet m_chine mit gleichem u-Wert) ist der Verlauf der UVSnake chine regelmäßig.
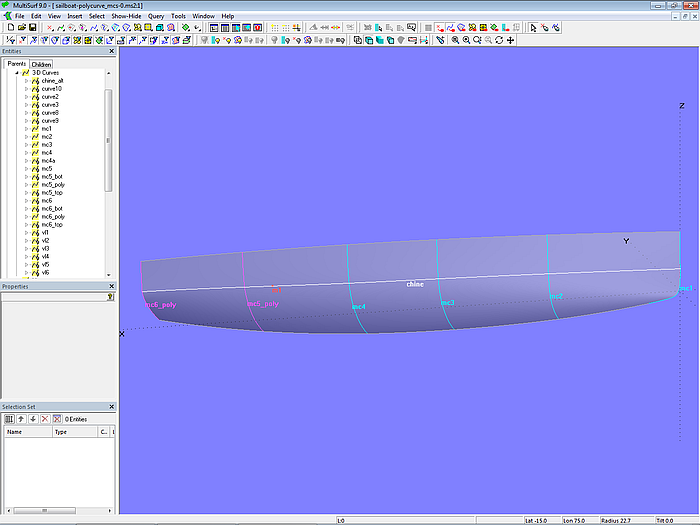
Modell sailboat-polycurve_mc-0s.ms2 – C-spline Lofted Surface hull_w_chine mit durchgehenden B-spline-Mcs vorne und PolyCurve-Mcs im Heckbereich. End t-value gesetzt auf 0.296.
Sehen wir uns jetzt den Verlauf der u-Parameterkurven von Modell sailboat-polycurve_mcs-0.ms2 an.

Modell sailboat-polycurve_mcs-0.ms2 – u-Parameterkurven der C-spline Lofted Surface hull_w_chine (durchgehende B-spline-Mcs vorne und PolyCurves achtern)
Wie im Modell sailboat-subcurve_mcs-0.ms2 verlaufen die Lofting Curves unterhalb des Knicks nicht regelmäßig. Die Ursache ist die gleiche – die unterschiedliche Parameterverteilung der Heck-Mcs im Vergleich zur Parametrisierung der vorderen Mcs. Da wir von der Fläche hull_fair wissen, dass diese Mcs eine regelmäßige Anordnung ihrer Cps in Längsrichtung haben, und folglich auch eine regelmäßige Parameterverteilung, ist es naheliegend, diese Mcs nicht zu ändern, sondern nur die hinteren Mcs.
Wie beim 2-Flächen-Ansatz stehen zwei Vorgehensweisen zur Verfügung. Zum einen kann man die hinteren Mcs mc5_bot und mc6_bot mit SubCurves relabeln und diese jeweils als PolyCurve-Segment verwenden. Dies ist in Modell sailboat-polycurve_mcs-1.ms2 gezeigt.
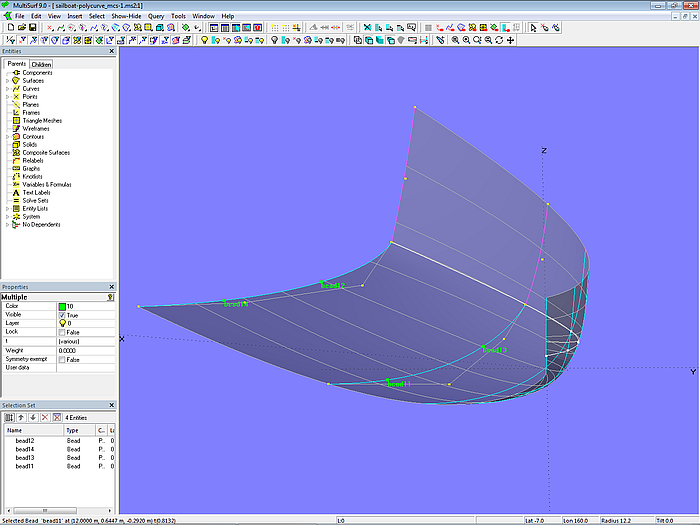
Modell sailboat-polycurve_mcs-1.ms2 – mc5_bot und mc6_bot mit SubCurves relabeled. Durch Verschieben der Beads bead1 und bead2 läßt sich der Verlauf der u-Parameterkurven ändern.
Zum anderen kann man mc5_bot und mc6_bot mit zusätzlichen Cps zu definieren. Modell sailboat-polycurve_mcs-2.ms2 verwendet einen Cps mehr.
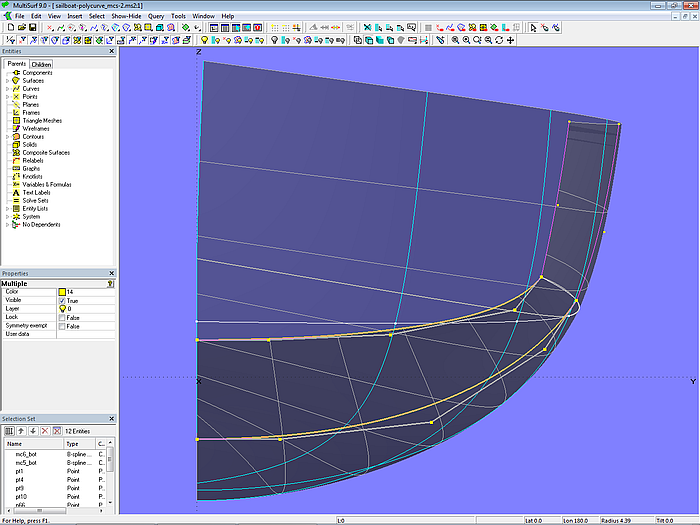
Modell sailboat-polycurve_mcs-2.ms2 – B-spline Curves mc5_bot und mc6_bot definiert mit zusätzlichem Kontrollpunkt
Vorteil:
Für den glatten Basisrumpf (hull_fair) kann die Vertexkurven-Methode angewendet werden. Die Mcs im Bereich des Rumpfes ohne Spantknick werden als Ganzes geformt, nicht getrennt. Sie sind richtungs- und krümmungsstetig. Die Parameterverteilung der Mcs ist ähnlich. Der Knickverlauf (chine) läßt sich leicht ändern, ohne dass sich gleichzeitig die Mc-Form ändert. Geringere Anzahl von Objekten = weniger Aufwand.
Nachteil:
Der Knickverlauf hängt von den „end t-values“ der PolyCurves ab. Man muß den Wert so wählen, dass eine strakende u-Parameterkurve der finalen Fläche entsteht. Das bedeutet Probierarbeit. Gegebenenfalls müssen die PolyCurves re-parametrisiert werden um strakende u-Parameterkurven zu erhalten.
Modell sailboat-polycurve_mcs-2.ms2
3 Beispiele
Die Rumpfform von Segelschiffen (Klipper, schneller Frachtsegler, klassische Yacht) hat häufig zwei markante Merkmale – ein rundes Heck mit einen auslaufenden Knick in Längsrichtung. Ein weiteres Beispiel ist der Rumpf eines Motorbootes.Um den Spantausfall zu begrenzen, hat der ansonsten rundspantige Rumpf einen Teilknick im Vorschiff.
3.1 Segelschiffsrumpf – rundes Heck mit auslaufendem Knick
Am Beispiel der Rumpfform einer Yacht soll gezeigt werden, wie man diese Geometrie nach dem Zwei-Flächen-Ansatz und dem Eine-Fläche-Ansatz modellieren kann.

Klassische Yacht – rundes Heck mit auslaufendem Knick
3.1.1 Zwei-Flächen-Ansatz – Masterkurven tangential verbunden
Wie in Abschnitt 1 beschrieben, wird bei dieser Vorgehensweise der Knick bis zum Bug verlängert, so dass eine in Längsrichtung verlaufende Kurve entsteht, die den Rumpf in zwei Flächen teilt. Bei manchen Schiffen ist die Kurve Seite Deck die Verlängerung der Knickkurve, so dass die obere Fläche das Schanzkleid darstellt.
Modell clipper-tangent_mcs.ms2 zeigt den Zwei-Flächen-Ansatz mit tangentialen Mcs im glatten Rumpfbereich. Die beiden Flächen topside und hull sind C-spline Lofted Surfaces, ihre Mcs sind B-spline Curves. Für die Fläche topside sind die Mcs mit je 3 Cps bestimmt (Mindestanzahl). Da topside eine schmale Fläche ist, liegen die Cps relativ dicht beieinander. Die Mcs der größeren Fläche hull werden mit 6 Cps geformt. Soweit wie möglich verlaufen die Mcs in Querschiffsrichtung. Letzter Cp einer Mc von topside ist zugleich erster Cp der Mc von hull. Die Mcs im Heckbereich stoßen mit einem Knick aneinander, die davor liegenden Mcs sind tangential zueinander. Durch korrespondierende Cps verlaufen C-spline Curves als Strakhilfskurven.
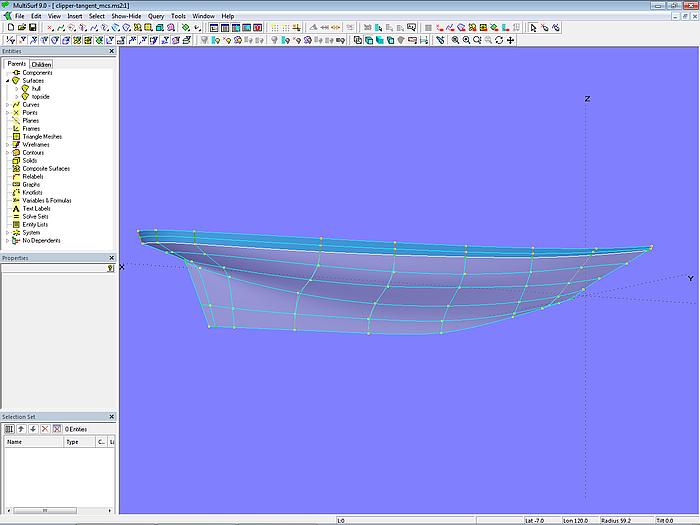
Modell clipper-tangent_mcs.ms2 – je 9 B-spline-Mcs stützen die C-spline Lofted Surfaces topside und hull. Vertexkurven verbinden korrespondierende Kontrollpunkte.
Damit der Knick im Heck zwischen den C-spline Lofted Surfaces topside und hull nach vorne ausläuft, müssen die Mcs in diesem Bereich tangential aneinander anschließen. Dazu ist auf jeder der vorderen Mcs für die Fläche hull ein Bead am Kurvenanfang (t = 0) angeordnet, von dem ein Tangent Point abhängt. Mit Cp1 und diesen beiden Punkten sind jeweils die Mcs von topside definiert. Durch den Tangent Point ist der tangentiale Anschluß der Mcs der oberen und unteren Fläche festverdrahtet.
Die Heck-Mcs sind wie Kantspanten angeordnet, um das runde Hinterschiff zu bilden. Die drei letzten Mcs der Fläche topside sind Lines (mc7_top, mc8_top, mc9_top). Die für die Vertexkurve vl2_top erforderlichen mittleren Kontrollpunkte an diesen Mcs sind Beads mit dem Parameterwert t = 0.5.
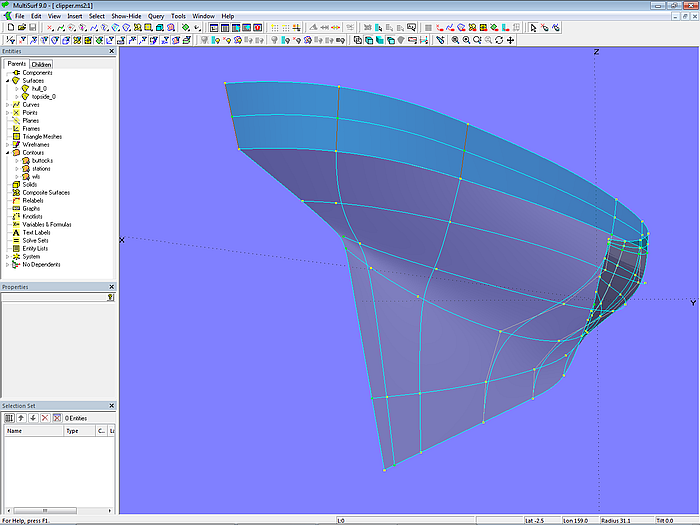
Modell clipper-tangent_mcs.ms2 – Zwei-Flächen-Ansatz. Im Heck-sind die Mcs als Kantspanten angeordnet.
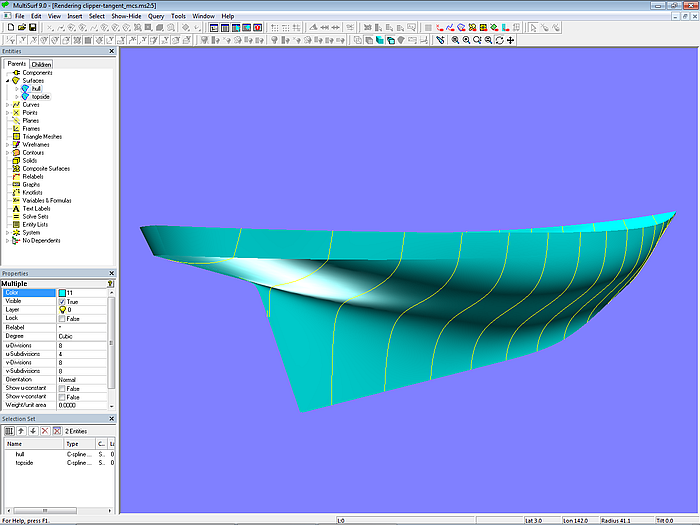
Modell clipper-tangent_mcs.ms2 – Zwei-Flächen-Ansatz
3.1.2 Eine-Fläche-Ansatz – Masterkurven verbunden zu PolyCurves
Im Modell clipper-polycurve_mcs.ms2 wird zunächst eine Basisfläche mit Mcs ohne Knick nach der Vertexkurven-Methode erzeugt (C-spline Lofted Surface hull_fair). Auf diese Weise erhalten wir einen strakenden Rumpf mit Masterkurven, deren Kontrollpunkte in Längsrichtung regelmäßig angeordnet sind und folglich eine regelmäßige Parameterverteilung haben. Wenn später an der eigentlichen Fläche hull_w_chine unharmonisch verlaufende u-Parameterkurven auftreten, muß an den von hull_fair übernommenen Mcs nichts geändert werden, lediglich die Parameterverteilung der PolyCurves muß geändert werden.
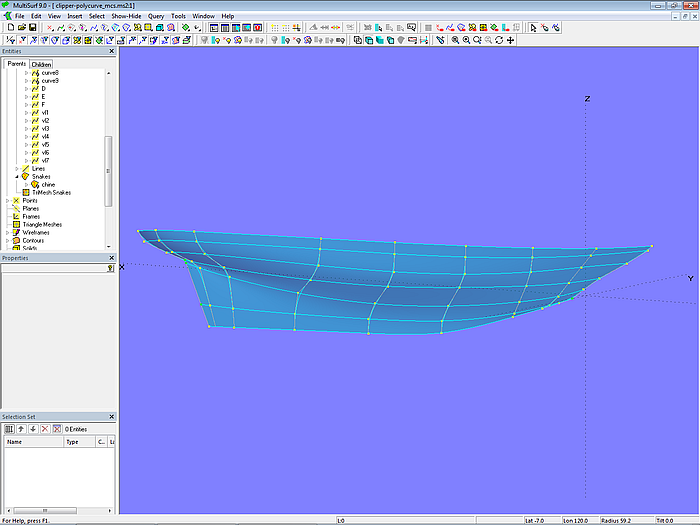
Modell clipper-polycurve_mcs.ms2 – Mcs und Vertexkurven der C-spline Lofted Surface hull_fair
Dann werden im Bereich des Hinterschiffs Mcs mit Knick für den oberen und unteren Rumpfbereich hinzugefügt, die zu PolyCurves verbunden werden (mc7_poly, mc8_poly, mc9_poly). Mit den vorderen Mcs und den PolyCurves im Heck ist die eigentliche Rumpffläche mit auslaufendem Knick definiert (C-spline Lofted Surface hull_w_chine).
Der end t-value für mc7_poly, mc8_poly und mc9_poly muß so gewählt werden, dass die UVSnake chine strakend verläuft. Er muß an allen PolyCurves der gleiche sein.

Modell clipper-polycurve_mcs.ms2 – Teilstücke der Heck-Masterkurven

Modell clipper-polycurve_mcs.ms2 – Teilstücke zusammengefügt zu PolyCurves
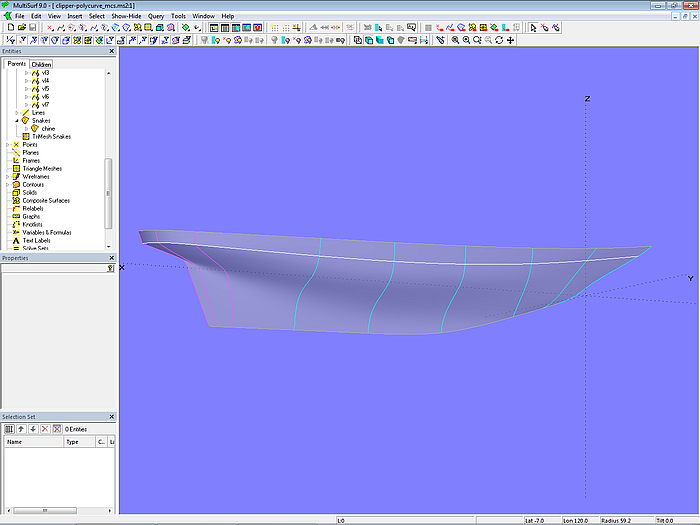
Modell clipper-polycurve_mcs.ms2 – von Ober- bis Unterkante Rumpf durchlaufende Mcs stützen die C-spline Lofted Surface hull_w_chine. Die vorderen Mcs sind B-spline Curves, die drei hinteren Mcs sind PolyCurves.
Wenn wir uns die u-Parameterkurven ansehen, fällt ein etwas unharmonischer Verlauf im unteren Bereich des Hinterschiffes auf.
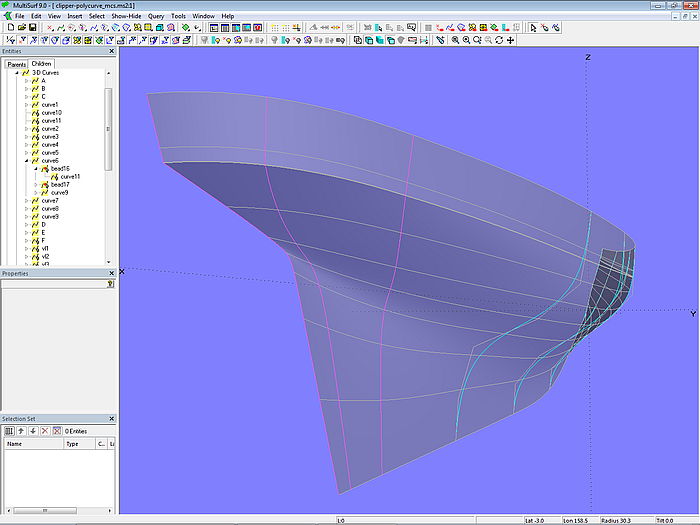
Modell clipper-polycurve_mcs.ms2 – unharmonischer Verlauf der unteren u-Parameterkurven im Hinterschiff
Um diesen Verlauf zu korrigieren, wird die Parameterverteilung von mc7_bot mit der SubCurve mc7_hull_sub und den inneren Beads bead1 und bead2 relabeled.
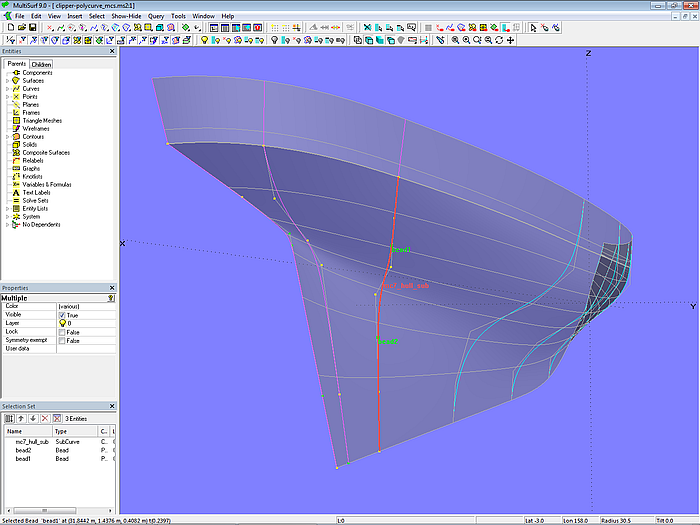
Modell clipper-polycurve_mcs.ms2 – regelmäßiger Verlauf der u-Parameterkurven durch SubCurve-Relabel
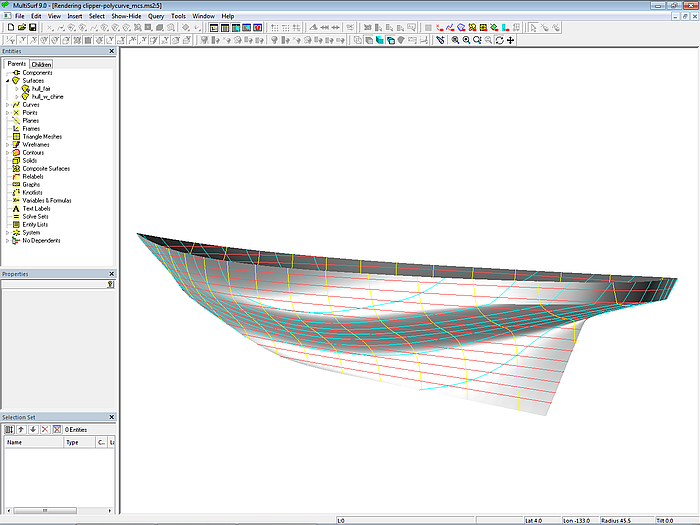
Modell clipper-polycurve_mcs.ms2
3.2 Motorbootrumpf – auslaufender Knick im Vorschiff
Ein weiteres Beispiel ist der Rumpf eines Motorboots. Hier befindet sich der auslaufende Knick im Vorschiff, um den Spantausfall zu kompensieren.
3.1.1 Zwei-Flächen-Ansatz – Masterkurven tangential verbunden
In Modell powerboat-tangent_mcs.ms2 ist der Rumpf nach dem Zwei-Flächen-Ansatz modelliert. Das heißt, der auslaufende Knick im Vorschiff erstreckt sich über die ganze Länge und teilt den Rumpf in die beiden C-spline Lofted Surface topside und hull. Beide Flächen haben jeweils die gleich Anzahl Mcs, die bis auf den Knickbereich mit Hilfe von Tangent Points tangential verbunden sind.
Bei dieser Konstruktion des Modells läßt sich die Vertexkurven-Methode zum Straken (siehe Anhang) verwenden. Die Knickkurve ist gleichzeitig eine Vertexkurve (C-spline Curve vl3_chine). Ihr Verlauf wird durch die entsprechenden Cps direkt bestimmt.
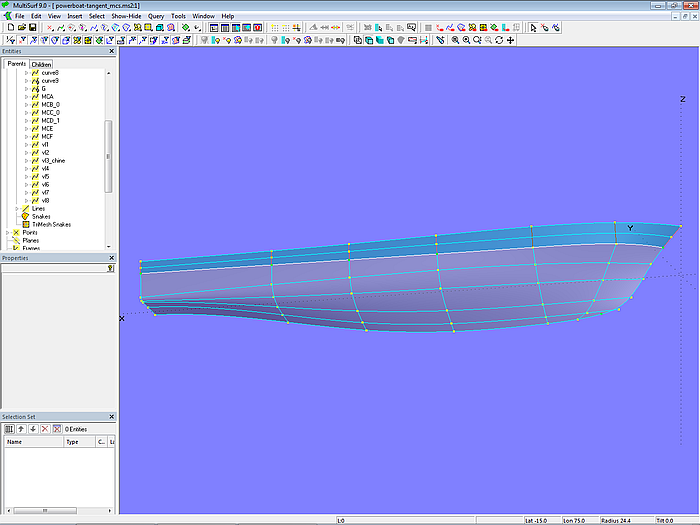
Modell powerboat-tangent_mcs.ms2 – Masterkurven und Strakhilfskurven der C-spline Lofted Surfaces topside und hull
3.1.2 Eine-Fläche-Ansatz – Masterkurven verbunden zu PolyCurves
In Modell powerboat-polycurve_mcs.ms2 ist der Rumpf nach dem Eine-Fläche-Ansatz modelliert. Von Ober- bis Unterkante Rumpf durchlaufende Mcs stützen die Fläche. Die Mcs im Knickbereich sind PolyCurves, die anderen Mcs sind B-spline Curves.
Auch hier gibt es als Ausgangspunkt eine Basisfläche ohne Knick, die C-spline Lofted Surface hull_fair. Alle Mcs sind B-spline Curves mit gleicher Anzahl Cps und gleichem Grad. Darum wird zum Straken die Vertexkurven-Methode genutzt.
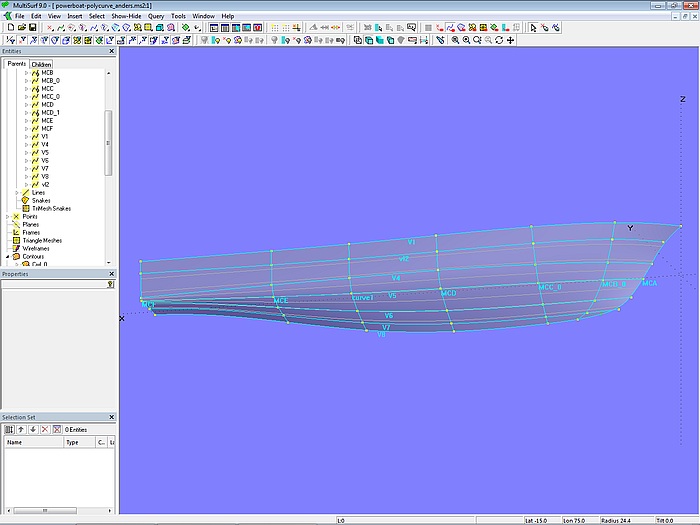
Modell powerboat-polycurve_mcs – glatte Basisfläche hull_fair mit durchlaufenden Mcs und Strakhilfskurven
Im Bereich des Vorschiffs werden nun Mcs mit Knick für den oberen und unteren Rumpfbereich hinzugefügt und diese dann zu PolyCurves verbunden (mc2_poly, mc3_poly).

Modell powerboat-polycurve_mcs – Teilstücke der Vorschiffs-Masterkurven

Modell powerboat-polycurve_mcs – Teilstücke verbunden zu PolyCurves
Mit den PolyCurves im Bugbereich und den hinteren Mcs wird die eigentliche Rumpffläche mit auslaufendem Knick erzeugt (C-spline Lofted Surface hull_w_chine). Der end t-value für mc2_poly und mc3_poly muß passend gewählt werden, damit die UVSnake chine strakend verläuft. An beiden PolyCurves muß der Wert gleich sein.
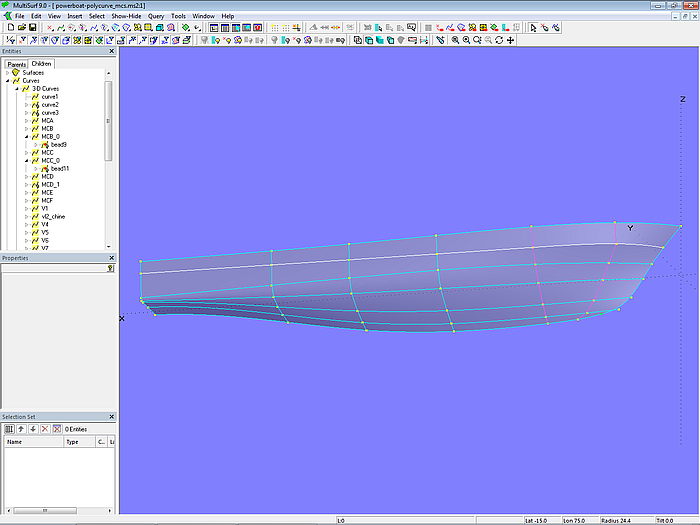
Modell powerboat-polycurve_mcs.ms2 – die Mcs der C-spline Lofted Surface hull_w_chine im Knickbereich sind PolyCurves.
Wie in den Modellen sailboat-polycurve_mcs-1.ms2 und clipper-polycurve_mcs.ms2 muß der Verlauf der u-Parameterkurven kontrolliert werden. Am einfachsten ist es, die Mcs mc5_bot und mc6_bot mit SubCurves zu relabeln und diese für die PolyCurve-Segmente zu verwenden. In Modell powerboat-polycurve_mcs.ms2 ist diese Konstruktion gewählt.
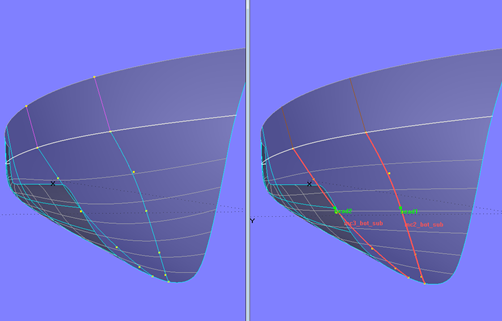
Modell powerboat-polycurve_mcs.ms2 – links: unregelmäßiger Verlauf der u-Parameterkurven; rechts: regelmäßiger Verlauf der u-Parameterkurven durch SubCurve-Relabel
Modell powerboat-polycurve_mcs.ms2
4 Zusammenfassung
Im vorliegenden Tutorium werden Methoden gezeigt, wie sich Rümpfe mit einem Knick in der Spantform modellieren lassen.
Der Zwei-Flächen-Ansatz – separate Mcs
Mcs außerhalb des Knickbereichs stoßen tangential zusammen. Regelmäßiger Verlauf der Parameterkurven durch Vertexkurven-Methode. Knickkurve gleich Vertexkurve.
Der Zwei-Flächen-Ansatz – geteilte Mcs
Durchlaufende Mcs außerhalb des Knickbereichs aufteilen in SubCurves. Mcs im Knickbereich müssen relabeled werden, damit Parameterkurven straken.
Der Eine-Fläche-Ansatz – durchlaufende Mcs und PolyCurves
Durchlaufende Mcs und PolyCurves im Knickbereich. PolyCurve-Segmente im Knickbereich müssen relabeled werden, damit Parameterkurven straken.
Welche Methode für einen Rumpf mit auslaufendem Knick am zweckmäßigsten ist, hängt davon ab, wie groß der Anteil der glatten Rumpffläche im Vergleich zum Bereich mit Knick ist.
Bei den Beispielen der klassischen Yacht und dem Motorboot verläuft die Knickkurve in relativ geringem Abstand von der Rumpfoberkante. Der obere Flächenstreifen ist schmal im Vergleich zum unteren, der Knickbereichs ist relativ klein. Der Knick ist mehr oder weniger ein lokales Formmerkmal, der größere Anteil der Rumpffläche im Spantgurtmaß ist glatt. Dann ist der Eine-Fläche-Ansatz (durchlaufende Mcs und PolyCurves) naheliegend. Ausgehend von einem glatten Basisrumpf wird der Rumpf über PolyCurves im Knickbereich nach außen in die gewünschte Form „gedrückt“.
Verwendet man bei einer solchen Rumpfform (relativ kleiner Knickbereich) den Zwei-Flächen-Ansatz mit separaten Mcs, sind im glatten Rumpfbereich die Mcs für die schmale obere Fläche relativ kurz. Und da die Mcs für diese Fläche mit mindestens 3 Cps definiert werden müssen, liegen sie dicht beieinander. Zwar sind mit Hilfe von Tangent Points zusammengehörige Mcs fest tangential verbunden, aber wenn an den Mcs für die breitere untere Fläche etwas geändert wird, muß man die Cps nachjustieren. Entsprechende Feinjustierung ist erforderlich.

Kontrollpunkt-Verteilung. Links: durchlaufende Mcs. Rechts: tangential verbundene Mcs
Verwendet man bei einer Rumpfform mit Knickkurve nahe der Oberkante den Zwei-Flächen-Ansatz mit SubCurves von durchlaufenden Mcs, dann können deren Cps gleichmäßiger über den Kurvenverlauf verteilt werden.
Beim Beispiel des Segelbootsrumpfs ist der Abstand der Knickkurve von Oberkante Rumpf größer, sie liegt näher zur Spantmitte. Dann bieten sich beide Varianten des Zwei-Flächen-Ansatzes an.
5 Anhang – die Vertexkurven-Methode
Die Aufgabe beim Modellieren eines Rumpfes besteht nicht nur darin, eine Fläche in der gewünschten Form zu erzeugen, die Fläche muß auch glatt sein, sie muß straken. Ähnlich wie bei einem realen Rumpf in Klinker-, Karweel- oder Leistenbauweise mit seinen harmonisch verlaufenden Planken ist eine C-spline Lofted Surface glatt, wenn ihre erzeugenden Lofting Curves (ihre "Planken“) straken.
Der Verlauf der Lofting Curves wird angezeigt, wenn im Properties-Manager in den Eigenschaften einer Lofted Surface „Show u-constant“ auf „True“ gesetzt ist. Dann wird die mit der Eigenschaft „“u-Divisions“ festgelegte Serie von Lofting Curves angezeigt. Diese Kurven werden auch als u-Parameterkurven der Fläche bezeichnet.
Der Verlauf der u-Parameterkurven hängt von der Parametrisierung der Masterkurven ab. Haben die Mcs den gleichen Typ, die gleiche Anzahl Cps und sind die Cps harmonisch angeordnet, verlaufen auch die u-Parameterkurven regelmäßig.
Ein einfacher Weg, um Cps harmonisch anzuordnen, besteht darin, alle korrespondierenden Cps der Mcs mit C-spline Curves zu verbinden. Diese Kurven werden als Vertexkurven bezeichnet. Sie zeigen, wie sich die Position einander entsprechender Cps vom Bug zum Heck hin verändert. Vertexkurven sind also Hilfskurven zum Straken einer C-spline Lofted Surface. Verlaufen sie in harmonischer, regelmäßiger Weise, ist die Fläche glatt.

Bei einer C-spline Lofted Surface besteht ein enger Zusammenhang zwischen dem Verlauf ihrer u-Parameterkurven und dem Verlauf der Vertexkurven.
Eine der Voraussetzungen für die Vertexkurven-Methode – alle Mcs müssen die gleiche Anzahl von Cps haben – erzwingt, dass die Mc mit der kompliziertesten Form die notwendige Anzahl der Cps bestimmt. Obwohl andere Mcs mit weniger Punkten definiert werden könnten, muß die erforderliche höhere Anzahl verwendet werden.
Dieser Nachteil wird mehr als aufgewogen durch die Möglichkeit, mit der Vertexkurven-Methode schnell und visuell verständlich den Strak einer C-spline Lofted Suface zu kontrollieren.
Die Modellieraufgabe hat also zwei Seiten - man muß die Cps an allen Mcs so anordnen, dass sich die gewünschte Rumpfform ergibt und gleichzeitig die Vertexkurven einen strakenden Verlauf annehmen.
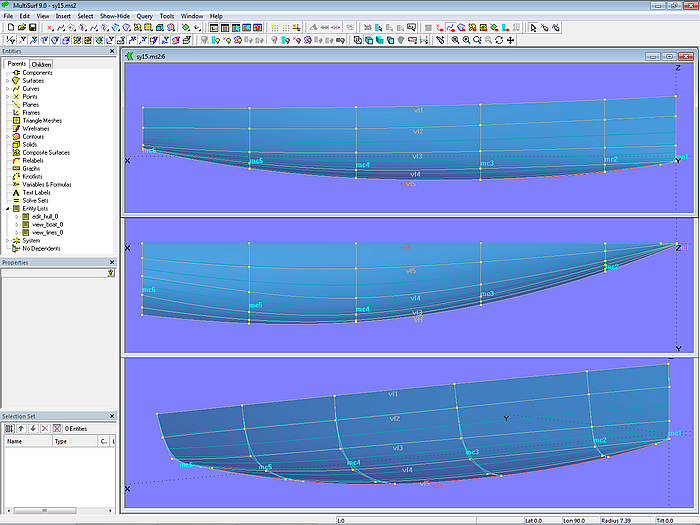
Vertexkurven als Strakhilfe
Es sei betont, dass unregelmäßige u-Parameterkurven nicht zwingend ein Anzeichen dafür ist, daß die Fläche nicht strakt. Man stelle sich einen glatten weißen Rumpf vor, auf den mit schwarzem Stift Längskurven gemalt werden. Wie krumm diese auch immer sein mögen, der Rumpf bleibt glatt.
Das Modellieren von Rümpfen nach der Vertexkurven-Methode ist jedoch viel einfacher und schneller, als bei unähnlichen Mcs (weil unterschiedlich im Typ, Grad oder Anzahl der Cps) durch Relabeln zu versuchen, regelmäßig verlaufende u-Parameterkurven zu erzeugen, oder ständig zu prüfen, ob die Fläche nicht trotzdem glatt ist, obwohl die u-Parameterkurven nicht straken.
======================================================================================