Remarks on Hull Surfaces
by Reinhard Siegel
Extract from:
On Modeling Classic Sailing Yacht Hulls
Some variations of the round bilged hull theme
Passive control points
In a C-spline Lofted Surface the lofting curve is a C-spline Curve, the mathematical formulation of a batten curve. A real batten can break, but given a sufficient number of cps a C-spline Curve can be bent into any shape (except breaks in slope). Transfered to the lofted surface this means: given enough mcs any shape with continous longitudinal slope is possible.
This approach is used in the model RWS28.ms2, a 28 ft wooden schooner hull (by courtesy of Edward Stanley, AeroHydro Inc.). The mcs define the hull surface from the sheer to the rabbet curve. Except the one for the bow the B-spline mcs run transversely. Each is supported by 8 cps, so vertex curves can be drawn.
Obviously the most complex curve is the rabbet (vertex curve 8): it runs straight along the keel, so does the stern overhang, and there is quite some curvature when bending away from the keel towards the rudder post. To shape the rabbet to the wish of the designer it takes 16 points (red colored points in the screen image). Note, that some points are closely spaced, especially at the begin or end of areas of high curvature, in order to avoid oscillation. 16 points for the definition of the rabbet curve means 16 mcs.
In comparison the sheer curve is more simple. 11 cps can define it (4 of them are close nearby at the stern to bend the sheer continuously into the transom top edge). Thus we have the situation, where one prominent curve requires many mcs, the other one considerably less. The trick in this model is to create vertex curves just with the individually necessary number of points: 8 cps are used for vertex curves 2 through 6, curve 7 is based on 10 points. The fore and aft position of all these cps correspond to those for the rabbet curve.
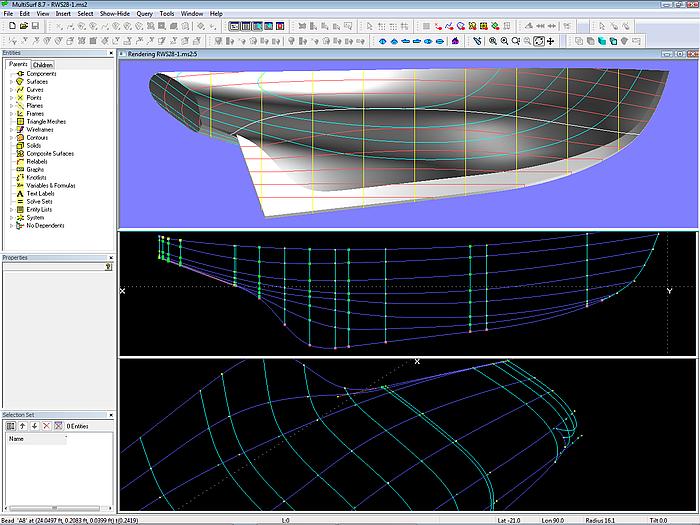
28 ft schooner (by courtesy of Edward Stanley, AeroHydro Inc.): system of master curves and vertex curves. Although the C-spline Lofted Surface is supported by 16 mcs, about half of the cps are Intersection Beads on the vertex curves, thus are automatically positioned.
It is obvious to refer to these points as active cps. In contrast to the passive cps (green colored points), which are derived by intersecting the vertex curves at the respective mc position. So we have a system of many mcs, but some of them have just one or two active cps, all their other cps are Intersection Beads on the vertex curves. Only the active cps need to be positioned by the user in order to form the mcs and at the same time keep the vertex curves fair.
Many mcs does not necessarily mean expensive adjustment of many cps. The use of vertex curves - with the minimum of cps required to achieve the wanted local shape - in combination with passive cps saves much work.
End of extract.
Model pwb-1.ms2
Another example for this hull construction method with C-spline Lofted Surfaces is model pwb-1.ms2 (by courtesy of AeroHydro Inc.). The hull surface is supported by 16 mcs, each a degree 3 B-spline Curve with 7 cps.

Model pwb-1.ms2 – extensive use of passive control points for mastercurves
Note the close arrangement of mcs where the fairbody is severely curved at the transition of keel to sternpost. end of the rabett configuration. Just a few of the cps are free and active ones, the majority are Intersection Beads on vertex curves or help lines.
Surface extension
It can happen during the design process that the transom is moved further aft as assumed initially. If the hull surface ends in front of the new transom position, the hull surface can be extended easily.
Put a magnet aft of the hull end, then create a UVSnake in the transeverse direction with this magnet as support. Next create the EdgeSnake along the stem of the hull. Finally define a SubSurface between EdgeSnake and UVSnake.
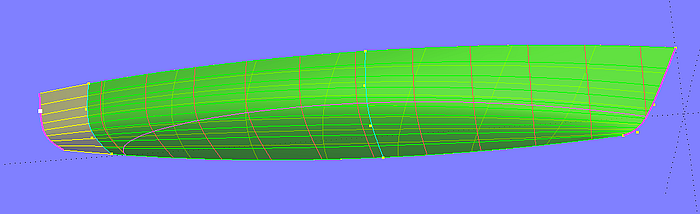
Model hull_extended-1.ms2 – SubSurface entity spanned between stem edge and UVSnake aft of stern
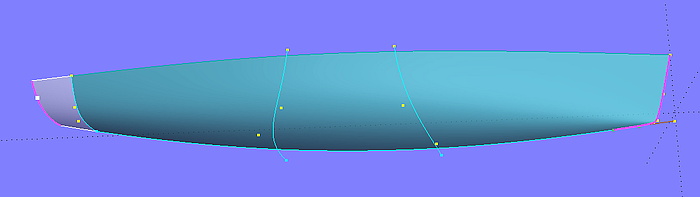
Model hull_extended-2.ms2 – SubSurface entity spanned between stem edge and UVSnake aft of stern
======================================================================================